题目内容
已知某几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个半圆柱与一个直三棱柱组合而成的几何体,计算出底面面积和高,代入柱体体积公式,可得答案.
解答:
解:由三视图可知该几何体是由一个半圆柱与一个直三棱柱组合而成的几何体,
∵圆柱的底面直径为2,高为2,
棱柱的底面是边长为2的等边三角形,高为2,
于是该几何体的体积为V=[
(π×12)+
×2×
]×2=π+2
.
故选:C
∵圆柱的底面直径为2,高为2,
棱柱的底面是边长为2的等边三角形,高为2,
于是该几何体的体积为V=[
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选:C
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若E为线段PF的中点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
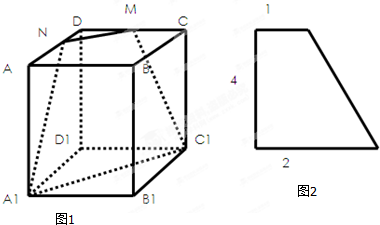
如图1所示,长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1,它的正视图、侧视图均为图2所示的直角梯形,则该几何体的体积为( )

A、
| ||
B、
| ||
| C、14 | ||
| D、10 |
对一切实数x,不等式ax2-ax-2<0恒成立,则实数a的取值范围是( )
| A、[-8,0] |
| B、(-8,0) |
| C、(-8,0] |
| D、[0,8) |
如图所示程序框图,其功能是输入x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )


| A、2个 | B、3个 | C、4个 | D、5个 |
从半径为r的圆内接正方形的4个顶点及圆心5个点中任取2个点,则这个点间的距离小于或等于半径的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|