题目内容
已知a1=4,an+1=
an,求an.
| n+2 |
| n |
考点:数列递推式
专题:等差数列与等比数列
分析:an+1=
an,a1=4,可得
=
,利用“累乘求积”即可得出.
| n+2 |
| n |
| an+1 |
| an |
| n+2 |
| n |
解答:
解:∵an+1=
an,a1=4,
∴
=
,
∴当n≥2时,an=
•
•
•…•
•
•
•a1
=
•
•
•…•
•
•
•4
=2n(n+1),
当n=1时,上式也成立.
∴an=2n2+2n.
| n+2 |
| n |
∴
| an+1 |
| an |
| n+2 |
| n |
∴当n≥2时,an=
| an |
| an-1 |
| an-1 |
| an-2 |
| an-2 |
| an-3 |
| a4 |
| a3 |
| a3 |
| a2 |
| a2 |
| a1 |
=
| n+1 |
| n-1 |
| n |
| n-2 |
| n-1 |
| n-3 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
=2n(n+1),
当n=1时,上式也成立.
∴an=2n2+2n.
点评:本题考查了“累乘求积”求数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
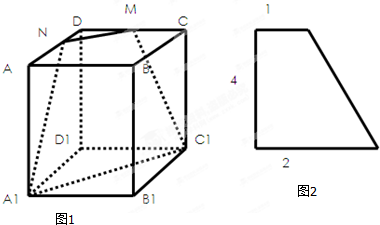
如图1所示,长方体AC1沿截面A1C1MN截得几何体DMN-D1A1C1,它的正视图、侧视图均为图2所示的直角梯形,则该几何体的体积为( )

A、
| ||
B、
| ||
| C、14 | ||
| D、10 |
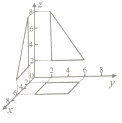
如图是一个四棱锥在空间直角坐标系xoz、xoy、yoz三个平面上的正投影,则此四棱锥的体积为( )

| A、94 | B、32 | C、64 | D、16 |
抛物线C1:x2=2y的焦点为F,以F为圆心C2交C1于A,B两点,交C1准线于C,D两点,若四边形ABCD是矩形,则C2的标准方程为( )
A、x2+(y-
| ||
B、(x-
| ||
C、x2+(y-
| ||
D、(x-
|