题目内容
4.已知ω为正整数,若函数f(x)=sin(ωx)在区间$(\frac{π}{6},\frac{π}{3})$上不单调,则最小的正整数ω=2.分析 由题意可得ω•$\frac{π}{6}$<$\frac{π}{2}$,且ω•$\frac{π}{3}$>$\frac{π}{2}$,由此求得最小正整数ω 的值.
解答 解:∵ω为正整数,函数f(x)=sin(ωx)在区间$(\frac{π}{6},\frac{π}{3})$上不单调,
∴ω•$\frac{π}{6}$<$\frac{π}{2}$,ω•$\frac{π}{3}$>$\frac{π}{2}$,∴$\frac{3}{2}$<ω<3,
则最小的正整数ω=2,
故答案为:2.
点评 本题主要考查正弦函数的图象特征,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.通过随机询问110名性别不同的大学生是否爱好体育,得到如表的列联表:
由公式算得:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}≈7.8$
附表:
参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表:
| P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99%以上的把握认为“爱好体育运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好体育运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别无关” |
12.已知函数h(x)=ax3-bx+1008,若h(-t)=2016,则h(t)等于( )
| A. | 1008 | B. | 0 | C. | 2016 | D. | 不确定 |
9.某四棱锥三视图如图所示,则该四棱锥体积为( )
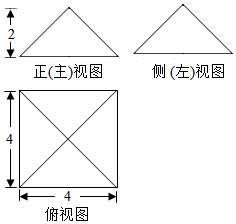

| A. | $\frac{16}{3}$ | B. | 16 | C. | 32 | D. | $\frac{32}{3}$ |
16.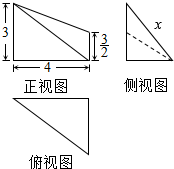 某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )
某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )
 某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )
某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )| A. | 5 | B. | 4 | C. | 2$\sqrt{7}$ | D. | $\sqrt{7}$ |
13.已知函数f(x)=(-x2+ax+b)(ex-e),当x>0时,f(x)≤0,则实数a的取值范围为( )
| A. | a>0 | B. | 0<a≤1 | C. | a≥1 | D. | a≤1 |