题目内容

16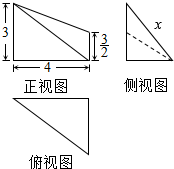．某几何体的三视图如图所示，若该几何体的体积为3$\sqrt{7}$，则侧视图中线段的长度x的值是（　　）
A．5B．4C．2$\sqrt{7}$D．$\sqrt{7}$

分析 作出直观图，根据体积求出侧视图三角形的底边即四棱锥的高即可．

解答 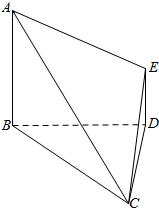解：由三视图可知几何体为侧放的四棱锥，作出直观图如图所示：
由三视图可知AB⊥平面BCD，DE⊥平面BCD，BD⊥CD，AB=3，DE=$\frac{3}{2}$．BD=4．
∴四棱锥的底面积S=$\frac{1}{2}×（3+\frac{3}{2}）×4$=9，
∴三棱锥的体积V=$\frac{1}{3}S•CD$=3CD=3$\sqrt{7}$．
∴CD=$\sqrt{7}$．
∴侧视图三角形的底边长为$\sqrt{7}$，由三视图的数量关系可知侧视图三角形的高为3，
∴x=$\sqrt{{3}^{2}+7}$=4．
故选：B．

点评 本题考查了棱锥的三视图和结构特征，属于基础题．

练习册系列答案
相关题目
6．椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左焦点为F1，上顶点为B2，右顶点为A2，过点A2作x轴的垂线交直线F1B2于点P，若|PA2|=3b，则椭圆的离心率为$\frac{1}{2}$．
7．已知函数$f（x）=\;{sin^2}\frac{x}{2}+\frac{{\sqrt{3}}}{2}sinx-\frac{1}{2}$．
（Ⅰ）求$f（\frac{π}{3}）$的值；
（Ⅱ）求函数f（x）在区间$[-\frac{π}{6}，\frac{5π}{6}]$上的最大值和最小值．
4．已知ω为正整数，若函数f（x）=sin（ωx）在区间$（\frac{π}{6}，\frac{π}{3}）$上不单调，则最小的正整数ω=2．
11．若直线l：ax+y-2-a=0在x轴和y轴上的截距相等，则直线l的斜率为（　　）
A．1B．-1C．-2或1D．-1或-2
1．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（1，0），设A，B为椭圆上关于原点对称的两点，AF的中点为M，BF的中点为N，原点O在以线段MN为直径的圆上，若直线AB的斜率k满足0＜k≤$\frac{\sqrt{3}}{3}$，则椭圆离心率e的取值范围为[$\frac{\sqrt{6}}{3}$，1）．
8．设|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，$\overrightarrow{a}$•$\overrightarrow{b}$=-6$\sqrt{2}$．求：
（1）＜$\overrightarrow{a}$，$\overrightarrow{b}$＞；
（2）（2$\overrightarrow{a}$-$\overrightarrow{b}$）•（$\overrightarrow{a}$+2$\overrightarrow{b}$）．
5．若函数y=f（x）的定义域为R+，且f（xy）=f（x）+f（y），f（8）=3，则f（2$\sqrt{2}$）等于$\frac{3}{2}$．
6．已知直线l⊥平面α，直线m?平面β，则下列四个命题中，正确的命题是（　　）
A．若α⊥β，则l∥mB．若α⊥β，则l⊥mC．若l⊥m，则α∥βD．若l∥m，则α⊥β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网