题目内容
8.已知函数f(x)=sin$\frac{πx}{2}$(x∈R),任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t).(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈[-2,0]时,求函数g(t)的解析式.
分析 (1)根据函数周期性和对称性的性质即可可先求出函数f(x)的最小正周期为4,
(2)由周期性得到g(t+4)=Mt-mt=g(t),然后探索-2≤t≤0的函数f(x)的最值,以及g(t)的解析式,即可得到结论.
解答 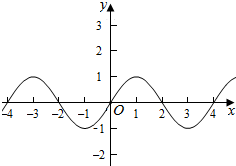 解:(1)函数的最小正周期T=$\frac{2π}{\frac{π}{2}}$=4,由$\frac{πx}{2}$=kπ+$\frac{π}{2}$得x=2k+1,k∈Z,即对称轴方程为x=2k+1,k∈Z.
解:(1)函数的最小正周期T=$\frac{2π}{\frac{π}{2}}$=4,由$\frac{πx}{2}$=kπ+$\frac{π}{2}$得x=2k+1,k∈Z,即对称轴方程为x=2k+1,k∈Z.
(2)画出函数f(x)的部分图象,如右图,
当-2≤t<-$\frac{3}{2}$,时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t)=sin$\frac{πt}{2}$,
∴g(t)=1+sin$\frac{πt}{2}$;
当-$\frac{3}{2}$≤t<-1时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t+1)=sin$\frac{πt+π}{2}$=cos$\frac{πt}{2}$,
∴g(t)=1+cos$\frac{πt}{2}$,
当-1≤t≤0时,f(x)在区间[t,t+1]上的最小值为f(t)=sin$\frac{πt}{2}$,最大值为f(t+1)=sin$\frac{πt+π}{2}$=cos$\frac{πt}{2}$,
∴g(t)=cos$\frac{πt}{2}$-sin$\frac{πt}{2}$.
即g(t)=$\left\{\begin{array}{l}{1+sin\frac{πt}{2},}&{-2≤t<-\frac{3}{2}}\\{1+cos\frac{πt}{2},}&{-\frac{3}{2}≤t<-1}\\{cos\frac{πt}{2}-sin\frac{πt}{2},}&{-1≤t≤0}\end{array}\right.$.
点评 本题主要考查函数的周期性以及应用,根据三角函数的图象和性质写出函数式,综合性较强,难度较大.

 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | -$\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | ±$\frac{2\sqrt{5}}{5}$ |
| A. | -4 | B. | -3 | C. | 1 | D. | 2 |
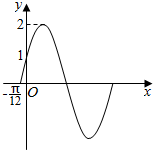 能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.