题目内容
6．已知三棱锥O-ABC，OA，OB，OC两两垂直，且OA=OB=$\sqrt{2}$，OC=1，P是△ABC上任意一点，设OP与平面ABC所成角为x，OP=y，则y关于x的函数关系图象为（ ）| A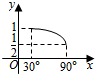． |  | B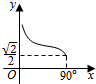． |  | C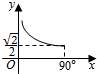． |  | D． |  |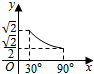
分析 作出点O在平面ABC的射影点O′，求出y=$\frac{1}{\sqrt{2}sinx}$，由此能求出结果．
解答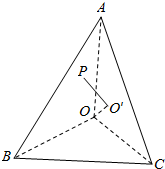 
解：作出点O在平面ABC的射影点O′，
∵三棱锥O-ABC，OA，OB，OC两两垂直，且OA=OB=$\sqrt{2}$，OC=1，
∴OO′=$\frac{\frac{1}{2}（\frac{\sqrt{6}}{2}）^{3}}{\frac{\sqrt{3}}{4}（\sqrt{3}）^{2}}$=$\frac{\sqrt{2}}{2}$，
∴|OP|=$\frac{O{O}^{'}}{sinx}$，即y=$\frac{1}{\sqrt{2}sinx}$，
当点P到A或B点位置时，x取得最小值$\frac{π}{6}$，故C、D不符合题意，
在A，B选基中，函数y=$\frac{1}{\sqrt{2}sinx}$的图象更符合B项．
故选：B．
点评 本题考查函数图象的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
16．已知数列{an}的前n项和为Sn，a1=1，Sn=2an+1，则当n＞1时，Sn=（ ）
| A． | （$\frac{3}{2}$）n-1 | B． | 2n-1 | C． | （$\frac{2}{3}$）n-1 | D． | $\frac{1}{3}$（$\frac{1}{{2}^{n-1}}$-1） |
17．已知m、n是两条不同直线，α、β是两个不同平面，给出下列命题，其中正确的是（ ）
| A． | 若α∩β=m，n?α，n⊥m，则α⊥β | B． | 若m∥β，n∥β，m、n?α，则α∥β | ||
| C． | 若m⊥α，n⊥β，m⊥n，则α⊥β | D． | 若m∥α，n∥β，m∥n，则α∥β |
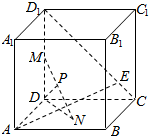已知棱长为3的正方体ABCD-A1B1C1D1中，长为2的线段MN的一端点M在DD1上运动，另一个端点N在底面ABCD上运动，动点E在线段CD1上，则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$．