题目内容
如图，在平面四边形ABCD中，AD=1，CD=2，AC=| 7 |
（Ⅰ）求cos∠CAD的值；
（Ⅱ）若cos∠BAD=-
| ||
| 14 |
| ||
| 6 |
考点：解三角形的实际应用
专题：解三角形
分析：（Ⅰ）利用余弦定理，利用已知条件求得cos∠CAD的值．
（Ⅱ）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．
（Ⅱ）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．
解答：
解：（Ⅰ）cos∠CAD=
=
=
．
（Ⅱ）∵cos∠BAD=-
，
∴sin∠BAD=
=
，
∵cos∠CAD=
，
∴sin∠CAD=
=
∴sin∠BAC=sin（∠BAD-∠CAD）=sin∠BADcos∠CAD-cos∠BADsin∠CAD=
×
+
×
=
，
∴由正弦定理知
=
，
∴BC=
•sin∠BAC=
×
=3
| AC2+AD2-CD2 |
| 2•AD•AC |
| 1+7-4 | ||
2×1×
|
2
| ||
| 7 |
（Ⅱ）∵cos∠BAD=-
| ||
| 14 |
∴sin∠BAD=
1-
|
3
| ||
| 14 |
∵cos∠CAD=
2
| ||
| 7 |
∴sin∠CAD=
1-
|
| ||
| 7 |
∴sin∠BAC=sin（∠BAD-∠CAD）=sin∠BADcos∠CAD-cos∠BADsin∠CAD=
3
| ||
| 14 |
2
| ||
| 7 |
| ||
| 14 |
| ||
| 7 |
| ||
| 2 |
∴由正弦定理知
| BC |
| sin∠BAC |
| AC |
| sin∠ABC |
∴BC=
| AC |
| sin∠ABC |
| ||||
|
| ||
| 2 |
点评：本题主要考查了正弦定理和余弦定理的综合运用，三角函数恒等变换的应用．考查了学生对基础知识的综合运用．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
抛物线y=
x2的准线方程是（ ）
| 1 |
| 4 |
| A、y=-1 | B、y=-2 |
| C、x=-1 | D、x=-2 |
设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论中正确的是（ ）
| A、f（x）g（x）是偶函数 |
| B、|f（x）|g（x）是奇函数 |
| C、f（x）|g（x）|是奇函数 |
| D、|f（x）g（x）|是奇函数 |
随机掷两枚质地均匀的骰子，它们向上的点数之和不超过5的概率记为p1，点数之和大于5的概率记为p2，点数之和为偶数的概率记为p3，则（ ）
| A、p1＜p2＜p3 |
| B、p2＜p1＜p3 |
| C、p1＜p3＜p2 |
| D、p3＜p1＜p2 |
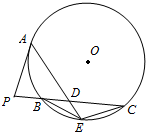如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E，证明：