题目内容
18.若函数$f(x)=sin(ωπx-\frac{π}{6})(ω>0)$的最小正周期为$\frac{1}{5}$,则$f(\frac{1}{3})$的值为-$\frac{1}{2}$.分析 利用正弦函数的周期性求得ω,再利用诱导公式求得$f(\frac{1}{3})$的值.
解答 解:∵函数$f(x)=sin(ωπx-\frac{π}{6})(ω>0)$的最小正周期为$\frac{2π}{ωπ}$=$\frac{1}{5}$,∴ω=10,
则$f(\frac{1}{3})$=sin(10π•$\frac{1}{3}$-$\frac{π}{6}$)=sin$\frac{19π}{6}$=sin$\frac{7π}{6}$=-sin$\frac{π}{6}$=-$\frac{1}{2}$,
故答案为:$-\frac{1}{2}$.
点评 本题主要考查正弦函数的周期性,利用诱导公式求三角函数的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知集合A={x|0<x<2},B={x|x2-1>0},那么A∩B=( )
| A. | {x|0<x<1} | B. | {x|1<x<2} | C. | {x|-1<x<0} | D. | {x|-1<x<2} |
8.若椭圆$\frac{{x}^{2}}{5}$+y2=1的左、右焦点恰好是双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的左、右顶点,则双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
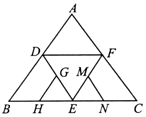 如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论: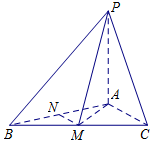 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点. 某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.
某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.