题目内容
求函数f（x）=
在x=0附近的平均变化率．
|
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：利用平均变化率公式，结合函数f（x）的解析式，求出f（x）在x=0附近的平均变化率即可．
解答：
解：x≤0时，函数f（x）=x2+2x在x=0附近的平均变化率
=
=△x+2；
x＞0时，函数f（x）=x+1在x=0附近的平均变化率
=
=1+
．
| △y |
| △x |
| (△x)2+2△x |
| △x |
x＞0时，函数f（x）=x+1在x=0附近的平均变化率
| △y |
| △x |
| △x+1 |
| △x |
| 1 |
| △x |
点评：本题考查了求分段函数在某一点附近的平均变化率问题，是基础题目．
练习册系列答案
相关题目
执行如图所示的算法，则输出的结果是（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
若不等式x2-px+q=0的解集为（-
，
），则不等式qx2+px+1＞0的解集为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| A、（-3，2） | ||||
| B、（-2，3） | ||||
C、（-
| ||||
D、（-
|
已知函数f（x）的导函数的图象如图所示，则下列判断中正确的是（ ）
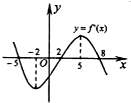
| A、函数f（x）在区间（-2，2）内单调递增 |
| B、函数f（x）在区间（-5，2）内单调递减 |
| C、函数f（x）在区间（5，8）内单调递减 |
| D、函数f（x）在区间（-2，5）内为单调函数 |
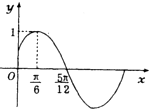已知函数f（x）=Asin（ωx+φ）（a＞0，ω＞0，|φ|＜| π |
| 2 |
A、f（x）=sin（3x+
| ||
B、f（x）=sin（2x+
| ||
C、f（x）=sin（x+
| ||
D、f（x）=sin（2x+
|