题目内容
已知函数f(x)=2αcos2x+bsinxcosx,且f(0)=2,f(
)
+
.
(1)求函数f(x)的单调减区间和对称轴方程;
(2)求函数f(x)取得最大值和最小值时对应的x的集合.
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
(1)求函数f(x)的单调减区间和对称轴方程;
(2)求函数f(x)取得最大值和最小值时对应的x的集合.
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:(1)由f(0)=2可求得a=1,再由f(
)=
+
可求得b=2,从而可得y=f(x)的解析式,利用正弦函数的性质可求函数f(x)的单调减区间和对称轴方程;
(2)利用f(x)=
sin(2x+
)+1,可求得函数f(x)取得最大值和最小值时对应的x的集合.
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
(2)利用f(x)=
| 2 |
| π |
| 4 |
解答:
解:(1)∵f(x)=a(1+cos2x)+
bsin2x,
又f(0)=2a=2,
∴a=1;
∴f(x)=1+cos2x+
bsin2x,
又f(
)=1+cos
+
bsin
=1-
+
b=
+
b=
+
,
∴b=2,
∴f(x)=1+cos2x+sin2x=
sin(2x+
)+1,
由
+2kπ≤2x+
≤2kπ+
(k∈Z)得:kπ-
≤x≤kπ+
(k∈Z),
∴f(x)的单调减区间为[kπ-
,kπ+
](k∈Z);
由2x+
=kπ+
(k∈Z)得:x=
+
(k∈Z),
∴函数f(x)的对称轴方程为:x=
+
(k∈Z);
(2)当2x+
=
+2kπ(k∈Z),即x=kπ+
(k∈Z)时,f(x)取得最大值
+1;
∴f(x)取得最大值时对应的x的集合为{x|x=kπ+
,k∈Z};
当2x+
=-
+2kπ(k∈Z),
即x=kπ-
(k∈Z)时,f(x)取得最小值-
+1;
∴f(x)取得最小值-
-1时对应的x的集合为{x|x=kπ-
,k∈Z}.
| 1 |
| 2 |
又f(0)=2a=2,
∴a=1;
∴f(x)=1+cos2x+
| 1 |
| 2 |
又f(
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
∴b=2,
∴f(x)=1+cos2x+sin2x=
| 2 |
| π |
| 4 |
由
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
∴f(x)的单调减区间为[kπ-
| π |
| 8 |
| 5π |
| 8 |
由2x+
| π |
| 4 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 8 |
∴函数f(x)的对称轴方程为:x=
| kπ |
| 2 |
| π |
| 8 |
(2)当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
∴f(x)取得最大值时对应的x的集合为{x|x=kπ+
| π |
| 8 |
当2x+
| π |
| 4 |
| π |
| 2 |
即x=kπ-
| 3π |
| 8 |
| 2 |
∴f(x)取得最小值-
| 2 |
| 3π |
| 8 |
点评:本题考查三角函数中的恒等变换应用,着重考查正弦函数的单调性、对称性与最值,考查方程思想与综合运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设A与B是相互独立事件,则下列命题正确的是( )
| A、A与B是互斥事件 | ||||
| B、A与B是对立事件 | ||||
C、
| ||||
D、
|
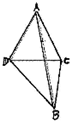 如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?
如图所示,某炮兵阵地位于点A处,两处观察所分别位于点D和C处,已知△ADC为正三角形,且DC=a,当目标在B点出现时,测量∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离AB是多少?