题目内容
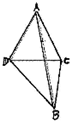如图所示，某炮兵阵地位于点A处，两处观察所分别位于点D和C处，已知△ADC为正三角形，且DC=a，当目标在B点出现时，测量∠CDB=45°，∠BCD=75°，则炮兵阵地与目标的距离AB是多少？考点：解三角形的实际应用
专题：应用题,解三角形
分析：在△BCD中利用正弦定理利用∠DBC和a，求得BC的值，进而在△ABC中利用BC和a，根据余弦定理求得AB．
解答：
解：在△BCD中，∠DBC=60°，
=
．
∴BC=
a
在△ABC中，∠BCA=135°，
AB2=（
a）2+a2-2×
a×a×cos135°=
a2
∴AB=
a．
故炮击目标的距离AB为
a．
| a |
| sin60° |
| BC |
| sin45° |
∴BC=
| ||
| 3 |
在△ABC中，∠BCA=135°，
AB2=（
| ||
| 3 |
| ||
| 3 |
5+2
| ||
| 3 |
∴AB=
| ||||
| 3 |
故炮击目标的距离AB为
| ||||
| 3 |
点评：本题主要考查了解三角形的实际应用．解三角形问题常用正弦定理，余弦定理，三角形面积公式等来解决．
练习册系列答案
相关题目
函数f（x）=|2x-1|，若a＜b＜c且f（a）＞f（c）＞f（b），则下列四个式子一成立的是（ ）
| A、a+c≥0 |
| B、a+c＜0 |
| C、b+c≥0 |
| D、b+c＜0 |
某几何体的三视图如图所示，则这个几何体的体积为（ ）
| A、4 | ||
B、
| ||
C、
| ||
| D、8 |