题目内容

7．已知向量法$\overrightarrow{{l}_{1}}$≠$\overrightarrow{0}$，λ∈R，$\overrightarrow{a}$=$\overrightarrow{{l}_{1}}$+λ$\overrightarrow{{l}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{l}_{2}}$，若向量$\overrightarrow{a}$和$\overrightarrow{b}$共线，则下列关系一定成立的是（　　）
A．λ=0B．$\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$C．$\overrightarrow{{l}_{1}}$∥$\overrightarrow{{l}_{2}}$D．$\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$或λ=0

分析 根据向量的共线定理即可判断．

解答 解：∵向量法$\overrightarrow{{l}_{1}}$≠$\overrightarrow{0}$，λ∈R，$\overrightarrow{a}$=$\overrightarrow{{l}_{1}}$+λ$\overrightarrow{{l}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{l}_{2}}$，
又∵向量$\overrightarrow{a}$和$\overrightarrow{b}$共线，存在实数k，使得$\overrightarrow{a}$=k$\overrightarrow{b}$，
∴$\overrightarrow{{l}_{1}}$+λ$\overrightarrow{{l}_{2}}$=k•2$\overrightarrow{{l}_{2}}$，
∴$\overrightarrow{{l}_{1}}$=（2k-λ）$\overrightarrow{{l}_{2}}$，
∵向量法$\overrightarrow{{l}_{1}}$≠$\overrightarrow{0}$，λ∈R，
∴$\overrightarrow{{l}_{1}}$∥$\overrightarrow{{l}_{2}}$，
故选：C．

点评 本题主要考查了向量的共线定理，同时考查了运算求解的能力，属于基础题．

练习册系列答案
相关题目
17．某中职学校高三年级5个班级的师生为庆祝教师节，每班学生准备了一个节目，已排成节目单，开演前又增加了3个教师节目，其中2个独唱节目，1个朗诵节目，如果将这3个节目插入原节目单中，要求教师的节目不排在第一个或最后一个，并且2个独唱节目不连续演出，则不同的插法有多少种？
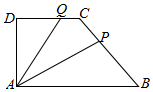18．如图，在直角梯形ABCD中，AB∥CD，AB=2，AD=DC=1，P是线段BC上一动点，Q是线段DC上一动点，$\overrightarrow{DQ}=λ\overrightarrow{DC}$，$\overrightarrow{CP}=（1-λ）\overrightarrow{CB}$，若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$，N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3（a-b）}，a＞b，ab=1}\right.}\right\}$．则M∩N=[$\frac{2\sqrt{3}}{3}$，2]．
15．已知函数f（x）=mx-$\frac{m}{x}$，g（x）=3lnx．
（1）当m=4时，求曲线f（x）=mx-$\frac{m}{x}$在点（2，f（2））处的切线方程；
（2）若x∈（1，$\sqrt{e}$]（e是自然对数的底数）时，不等式f（x）-g（x）＜3恒成立，求实数m的取值范围．
2．已知变量x，y，满足：$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$，则z=2x+y的最大值为4．
12．已知$\overrightarrow{a}$=t$\overrightarrow{{e}_{1}}$+（k2-1）$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=（2t+1）$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$，且$\overrightarrow{a}$∥$\overrightarrow{b}$，试求t关于k的函数．
19．己知函数f（x）=tanx-x（0＜x＜$\frac{π}{2}$）．
（1）试判断函数f（x）的单调性，并说明理由；
（2）若数列{an}满足0＜a1＜$\frac{π}{4}$，an+1=f（an），n∈N*，证明：0＜an+1＜an＜$\frac{π}{4}$．
16．设锐角△ABC的外接圆圆心为O，半径为25，弦AB=48，AC=40，则cos∠BAC的值为$\frac{3}{5}$，$\overrightarrow{OA}$$•\overrightarrow{OB}$+$\overrightarrow{OB}$$•\overrightarrow{OC}$+$\overrightarrow{OC}$$•\overrightarrow{OA}$=-877．
11．如图所示的程序运行后输出的结果是（　　）
A．-5B．-3C．0D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网