题目内容
平面α内有无数条直线与平面β平行,那么α∥β是否正确?说明理由.
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:根据空间面面平行的定义和性质即可得到结论.
解答:
解:当两个平面平行时符合平面α内有无数条直线都与平面β平行,
当两平面相交时,在α平面内作与交线平行的直线,也有平面α内有无数条直线都与平面β平行,
故平面α内有无数条直线与平面β平行,那么α∥β不一定正确.
当两平面相交时,在α平面内作与交线平行的直线,也有平面α内有无数条直线都与平面β平行,
故平面α内有无数条直线与平面β平行,那么α∥β不一定正确.
点评:本题主要考查面面平行的判断,比较基础.

练习册系列答案
相关题目
已知向量
=(3,1),
=(-2,
),则下列向量可以与
+2
垂直的是( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、(-1,2) |
| B、(2,-1) |
| C、(4,2) |
| D、(-4,2) |
在△ABC中,若
•(
-2
)=0,则△ABC的形状为 ( )
| AB |
| AB |
| AC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
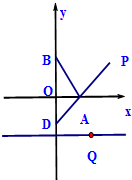 如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.
如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA. 已知P是圆O外一点,PE切圆O于点E,B、F是圆O上一点,PB交圆O于A点,EF∥AP,BE:BF=3:4,PE=4,则AB=
已知P是圆O外一点,PE切圆O于点E,B、F是圆O上一点,PB交圆O于A点,EF∥AP,BE:BF=3:4,PE=4,则AB=