题目内容
函数y=
的定义域是 ．
| log2(3-x) |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由根式内部的代数式大于等于0且对数型函数的真数大于0联立不等式组求解x的取值集合得答案．
解答：
解：要使函数游意义，x应满足：
，∴
，
解得x≤2．
∴函数的定义域为（-∞，2]．
故答案为：（-∞，2]．
|
|
解得x≤2．
∴函数的定义域为（-∞，2]．
故答案为：（-∞，2]．
点评：本题考查了函数的定义域及其求法，是基础题．
练习册系列答案
相关题目
命题“若A∩B=A，则A⊆B的逆否命题是（ ）
| A、若A∪B≠A，则A?B |
| B、若A∩B≠A，则A⊆B |
| C、若A?B，则A∩B≠A |
| D、若A?B，则A∩B≠A |
设f（x）=x2-4x（x∈R），则f（x）＜0的一个必要不充分条件是（ ）
| A、0＜x＜4 |
| B、x＜0或x＞4 |
| C、0≤x＜4 |
| D、0＜x＜3 |
k进制数32501（k），则k不可能是（ ）
| A、5 | B、6 | C、7 | D、8 |
已知集合M={x|-2＜x＜2}，N={x|-1＜x＜3}，则M∩N=（ ）
| A、{x|x＜-2} |
| B、{x|x＞3} |
| C、{x|-1＜x＜2} |
| D、{x|2＜x＜3} |
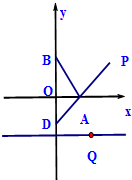如图，在平面直角坐标系中，O为坐标原点，点B（0，1），且点A（a，0）（a≠0）是x轴上动点，过点A作线段AB的垂线交y轴于点D，在直线AD上取点P，使AP=DA．