题目内容
已知公比不为1的等比数列{an}的首项a1=2,前n项和为Sn,且a4+S4,a5+S5,a6+S6成等差数列.
(1)求等比数列{an}的通项公式.
(2)对n∈N+,在an和an+1之间插入n个数,使这n+2个数成等差数列,记插入的这n个数的和为bn,求数列{bn}的前n项和Tn.
(1)求等比数列{an}的通项公式.
(2)对n∈N+,在an和an+1之间插入n个数,使这n+2个数成等差数列,记插入的这n个数的和为bn,求数列{bn}的前n项和Tn.
考点:数列的应用
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:本题(1)可以用首项和公比表示a4+S4,a5+S5,a6+S6,利用成等差条件,得到相应的方程,解方程得到本题结论;(2)利用(1)的结论,研究得到an和an+1之间的n个数,利用等差数列求和公式求和,得到bn,再求数列{bn}的前n项和Tn,得到本题结论.
解答:
解:(1)∵a4+S4,a5+S5,a6+S6成等差数列,
∴a5+S5-(a4+S4)=a6+S6-(a5+S5),
∴2a5-a4=2a6-a5,
∴2a6-3a5+a4=0.
∵数列{an}为等比数列,
∴a5=a4q,a6=2a4q2,
∴2q2-3q+1=0,
∴(2q-1)(q-1)=0.
∵数列{an}公比不为1,
∴q=
.
∴an=2×(
)n-1,
∴an=(
)n-2.
∴等比数列{an}的通项公式:an=(
)n-2.
(2)由(1)知:an+1=(
)n-1.
对n∈N+,在an和an+1之间插入n个数,分别记为:c1,c2,c3,…cn,
使得:an,c1,c2,c3,…cn,an+1成等差数列,
则bn=
=
=
.
∵数列{bn}的前n项和为Tn,
∴Tn=b1+b2+b3+…+bn
∴Tn=3×(
)+6×(
)2+9×(
)3+…+
.…①
Tn=3×(
)2+6×(
)3+9×(
)4…+
.…②
由①-②得:
Tn=3×(
)+[3×(
)2+3×(
)3+3×(
)4…+
]-
.…②
=
-
.
∴Tn=6-
,n∈N*.
∴数列{bn}的前n项和为:Tn=6-
,n∈N*.
∴a5+S5-(a4+S4)=a6+S6-(a5+S5),
∴2a5-a4=2a6-a5,
∴2a6-3a5+a4=0.
∵数列{an}为等比数列,
∴a5=a4q,a6=2a4q2,
∴2q2-3q+1=0,
∴(2q-1)(q-1)=0.
∵数列{an}公比不为1,
∴q=
| 1 |
| 2 |
∴an=2×(
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
∴等比数列{an}的通项公式:an=(
| 1 |
| 2 |
(2)由(1)知:an+1=(
| 1 |
| 2 |
对n∈N+,在an和an+1之间插入n个数,分别记为:c1,c2,c3,…cn,
使得:an,c1,c2,c3,…cn,an+1成等差数列,
则bn=
| (c1+cn)n |
| 2 |
| (an+an+1)n |
| 2 |
| 3n |
| 2n |
∵数列{bn}的前n项和为Tn,
∴Tn=b1+b2+b3+…+bn
∴Tn=3×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3n |
| 2n+1 |
由①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2n |
| 3n |
| 2n+1 |
=
| ||||
1-
|
| 3n |
| 2n+1 |
∴Tn=6-
| 3n+6 |
| 2n |
∴数列{bn}的前n项和为:Tn=6-
| 3n+6 |
| 2n |
点评:本题考查了等差数列、等比数列、以及数列的错位相减法求和,本题难度较大,计算量适中,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
命题“若A∩B=A,则A⊆B的逆否命题是( )
| A、若A∪B≠A,则A?B |
| B、若A∩B≠A,则A⊆B |
| C、若A?B,则A∩B≠A |
| D、若A?B,则A∩B≠A |
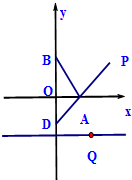 如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.
如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.