题目内容
已知数列{an}的前n项和为Sn,且a1+2a2+3a3+…+nan=(n-1)Sn+2n,n∈N+.
(1)求数列{an}的通项公式;
(2)证明:(1-
)(1-
)(1-
)…(1-
)>
.
(1)求数列{an}的通项公式;
(2)证明:(1-
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 5 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*),再写一式,两式相减,化简可得{Sn+2}是以4为首项,2为公比的等比数列,求出Sn=2n+1-2,即可得到结论.
(2)1-
=1-
=1-
,(1-
)(1-
)(1-
)…(1-
)=(1-
)(1-
)(1-
)…(1-
)>1-(
+
+…+
)即可得出证明.
(2)1-
| 1 | ||
|
| 1 |
| (2n)2 |
| 1 |
| 4n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 4n |
解答:
(1)解:∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*),①
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)Sn-1+2(n-1).②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
∴nan=n(Sn-Sn-1)-Sn+2Sn-1+2
∴nan=nan-Sn+2Sn-1+2.
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2).
∵S1+2=4≠0,∴Sn-1+2≠0,
∴{Sn+2}是以4为首项,2为公比的等比数列.
∴Sn+2=2n+1,
∴Sn=2n+1-2,
∴n≥2时,an=Sn-Sn-1=2n,
n=1时,a1=S1=2,也满足上式,
∴an=2n.
(2)证明:1-
=1-
=1-
,
∴(1-
)(1-
)(1-
)…(1-
)=(1-
)(1-
)(1-
)…(1-
)>1-(
+
+…+
)=1-
=1-
(1-
)>
>
.
∴(1-
)(1-
)(1-
)…(1-
)>
.
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)Sn-1+2(n-1).②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
∴nan=n(Sn-Sn-1)-Sn+2Sn-1+2
∴nan=nan-Sn+2Sn-1+2.
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2).
∵S1+2=4≠0,∴Sn-1+2≠0,
∴{Sn+2}是以4为首项,2为公比的等比数列.
∴Sn+2=2n+1,
∴Sn=2n+1-2,
∴n≥2时,an=Sn-Sn-1=2n,
n=1时,a1=S1=2,也满足上式,
∴an=2n.
(2)证明:1-
| 1 | ||
|
| 1 |
| (2n)2 |
| 1 |
| 4n |
∴(1-
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 4n |
| ||||
1-
|
| 1 |
| 3 |
| 1 |
| 4n |
| 2 |
| 3 |
| 2 |
| 5 |
∴(1-
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 5 |
点评:本题考查数列递推式,考查等比数列的证明及不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
k进制数32501(k),则k不可能是( )
| A、5 | B、6 | C、7 | D、8 |
已知向量
=(3,1),
=(-2,
),则下列向量可以与
+2
垂直的是( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、(-1,2) |
| B、(2,-1) |
| C、(4,2) |
| D、(-4,2) |
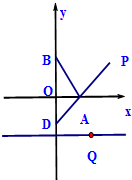 如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.
如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.