题目内容
已知直线l1∥l2,A是l1,l2之间的一定点,并且A点到l1,l2的距离分别为h1,h2,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC面积的最小值为 .
考点:点到直线的距离公式
专题:直线与圆
分析:过A作l1、l2的垂线,分别交l1、l2于E、F.设∠FAC=θ,由直角三角形中三角函数的定义,算出AC=
且AB=
,从而得到△ABC面积S=
AB•AC=
,利用正弦函数的有界性,可得θ=
时△ABC面积有最小值h1•h2.
| h1 |
| cosθ |
| h2 |
| sinθ |
| 1 |
| 2 |
| h1h2 |
| sin2θ |
| π |
| 4 |
解答:
解: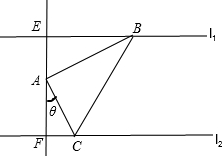 过A作l1、l2的垂线,分别交l1、l2于E、F,
过A作l1、l2的垂线,分别交l1、l2于E、F,
则AF=h1,AE=h2,
设∠FAC=θ,则Rt△ACF中,AC=
,
Rt△ABE中,∠ABE=θ,
可得AB=
,
∴△ABC面积为S=
AB•AC=
,
∵θ∈(0,
)
∴当且仅当θ=
时,sin2θ=1达到最大值1,
此时△ABC面积有最小值h1•h2,
故答案为:h1•h2
 过A作l1、l2的垂线,分别交l1、l2于E、F,
过A作l1、l2的垂线,分别交l1、l2于E、F,则AF=h1,AE=h2,
设∠FAC=θ,则Rt△ACF中,AC=
| h1 |
| cosθ |
Rt△ABE中,∠ABE=θ,
可得AB=
| h2 |
| sinθ |
∴△ABC面积为S=
| 1 |
| 2 |
| h1h2 |
| sin2θ |
∵θ∈(0,
| π |
| 2 |
∴当且仅当θ=
| π |
| 4 |
此时△ABC面积有最小值h1•h2,
故答案为:h1•h2
点评:此题考查了直角三角形中锐角三角函数定义,正弦函数的定义域及值域及二倍角的正弦函数公式,利用了数形结合的思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
空间直线a、b、c,平面α,则下列命题中真命题的是( )
| A、若a⊥b,c⊥b,则a∥c |
| B、若a∥α,b∥α,则a∥b |
| C、若a与b是异面直线,a与c是异面直线,则b与c也是异面直线 |
| D、若a∥c,c⊥b,则b⊥a |
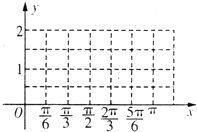 已知函数f(x)=sin(2ωx-
已知函数f(x)=sin(2ωx-