Question

如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，BC=

1

2

AD=1，PD=CD=2，Q为AD的中点，M为PC的中点．
（Ⅰ）证明：PA∥平面BMQ；
（Ⅱ）求三棱锥A-BMQ的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：计算题,证明题,空间位置关系与距离

分析：（1）连接AC交BQ于N，连接MN，由MN∥PA证明PA∥平面BMQ．（2）取CD中点K，连接MK，可证MK⊥底面ABCD，从而求出其体积．

解答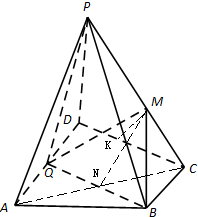： 解：（1）证明：连接AC交BQ于N，连接MN，
∵∠ADC=90°，Q为AD的中点，
∴N为AC的中点，
∵MN为△PAC的中位线，
故MN∥PA，
又∵PA?平面BMQ，MN?平面BMQ，
∴PA∥平面BMQ．
（2）取CD中点K，连接MK，
∴MK∥PD且MK=

1

2

PD=1，
又∵PD⊥底面ABCD，
∴MK⊥底面ABCD，
又∵BC=

1

2

AD=1，PD=CD=2，
∴AQ=1，BQ=2，
∴V_A-BMQ=V_M-ABQ=

1

3

•

1

2

•AQ•BQ•MK=

1

3

．

点评：本题考查了线面平行的判定定理，及几何体体积的求法，难点在于找到线线平行，及找到合适的底面与高以简化运算．