题目内容
已知函数f(x)=x2+bx+c(b,c∈R﹚.
(1)|f﹙1﹚|≤|f﹙-1﹚|≤
成立,求b2+c2的取值范围;
(2)若f(x)在区间(0,1)上有两个零点,求证:c2+﹙1+b﹚c≤
.
(1)|f﹙1﹚|≤|f﹙-1﹚|≤
| 1 |
| 4 |
(2)若f(x)在区间(0,1)上有两个零点,求证:c2+﹙1+b﹚c≤
| 1 |
| 16 |
考点:简单线性规划的应用,不等式的证明
专题:不等式的解法及应用
分析:(1)画出满足|f﹙1﹚|≤|f﹙-1﹚|≤
的可行域,结合b2+c2的几何意义,可得b2+c2的取值范围.
(2)若函数f(x)在区间(0,1)上有两个零点,为x1,x2(0<x1<x2<1),即f(0)=c=x1x2>0,f(1)=1+b+c=(1-x1)(1-x2)>0,进而结合基本不等式可得c2+﹙1+b﹚c≤
.
| 1 |
| 4 |
(2)若函数f(x)在区间(0,1)上有两个零点,为x1,x2(0<x1<x2<1),即f(0)=c=x1x2>0,f(1)=1+b+c=(1-x1)(1-x2)>0,进而结合基本不等式可得c2+﹙1+b﹚c≤
| 1 |
| 16 |
解答:
解:(1)∵|f﹙1﹚|≤|f﹙-1﹚|≤
,
∴|1+b+c|≤|1-b+c|≤
,
即
,
满足约束条件的可行域如下图所示:
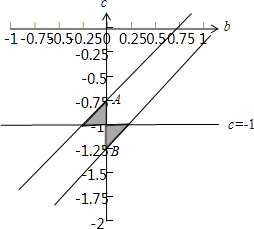
又∵b2+c2表示动点(b,c)到原点距离的平方,
由图可知:当b=0,c=-
时,b2+c2取最小值
,
当b=0,c=-
时,b2+c2取最大值
,
故b2+c2的取值范围为[
,
]
证明:(2)f(x)=x2+bx+c的两个零点为x1,x2(0<x1<x2<1),
则f(x)=(x-x1)(x-x2).
又f(0)=c=x1x2>0,f(1)=1+b+c=(1-x1)(1-x2)>0
∴c(1+b+c)=f(0)f(1),
而0<f(0)f(1)=x1x2(1-x1)(1-x2)≤
,
即c(1+b+c)=c2+﹙1+b﹚c≤
.
| 1 |
| 4 |
∴|1+b+c|≤|1-b+c|≤
| 1 |
| 4 |
即
|
满足约束条件的可行域如下图所示:
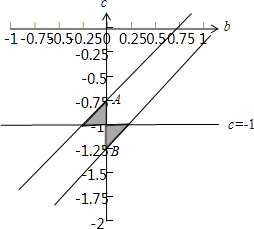
又∵b2+c2表示动点(b,c)到原点距离的平方,
由图可知:当b=0,c=-
| 3 |
| 4 |
| 9 |
| 16 |
当b=0,c=-
| 5 |
| 4 |
| 25 |
| 16 |
故b2+c2的取值范围为[
| 9 |
| 16 |
| 25 |
| 16 |
证明:(2)f(x)=x2+bx+c的两个零点为x1,x2(0<x1<x2<1),
则f(x)=(x-x1)(x-x2).
又f(0)=c=x1x2>0,f(1)=1+b+c=(1-x1)(1-x2)>0
∴c(1+b+c)=f(0)f(1),
而0<f(0)f(1)=x1x2(1-x1)(1-x2)≤
| 1 |
| 16 |
即c(1+b+c)=c2+﹙1+b﹚c≤
| 1 |
| 16 |
点评:本题考查的知识点是简单线性规划的应用,不等式的证明,是基本不等式,线性规划与不等式证明的综合应用,综合性强,计算量大,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列
,
,
,
,…的一个通项公式是( )
| 22+1 |
| 2 |
| 32+1 |
| 4 |
| 42+1 |
| 8 |
| 52+1 |
| 16 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,设直线l:y=k(x-2
如图,设直线l:y=k(x-2 如图,有两条相交直线成60°角的直路X′X,Y′Y,交点是O,甲、乙两人分别在OX,OY上,甲的起始位置距离O点3km,乙的起始位置距离O点1km,后来甲沿X′X的方向,乙沿Y′Y的方向,两人同时以4km/h的速度步行.
如图,有两条相交直线成60°角的直路X′X,Y′Y,交点是O,甲、乙两人分别在OX,OY上,甲的起始位置距离O点3km,乙的起始位置距离O点1km,后来甲沿X′X的方向,乙沿Y′Y的方向,两人同时以4km/h的速度步行. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC= 如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.
如图所示几何体是正方体ABCD-A1B1C1D1截去三棱锥B1-A1BC1后所得,点M为A1C1的中点.