题目内容
已知数列{an}的前n项和Sn=12-22+32-42+…+(-1)n+1n2,则S10= ,S27= ,Sn= .
考点:数列的求和
专题:等差数列与等比数列
分析:利用平方差公式展开可得:S10=12-22+32-42+…+92-102=(1-2)(1+2)+(3-4)(3+4)+…+(9-10)(9+10)再利用等差数列的前n项和公式即可得出.类比S10即可得出S27.对n分类讨论即可得出Sn.
解答:
解:S10=12-22+32-42+…+92-102
=(1-2)(1+2)+(3-4)(3+4)+…+(9-10)(9+10)
=-(1+2+3+…+10)
=-
=-55.
S27=12-22+32-42+…+252-262+272
=(1-2)(1+2)+(3-4)(3+4)+…+(25-26)(25+26)+272
=-(1+2+3+…+26)+272
=-
+272
=378.
当n为偶数2k(k∈Z)时,
S2k═12-22+32-42+…+(2k-1)2-(2k)2
=(1-2)(1+2)+(3-4)(3+4)+…+(2k-1-2k)(2k-1+2k)
=-(1+2+…+2k-1+2k)
=-
=-
.
当n为奇数2k-1(k∈Z)时,
S2k-1=S2k-(-1)2k+1(2k)2
=-
+(n+1)2
=
.
综上可得:Sn=(-1)n+1×
,(n∈N*).
故答案分别为:-55;378;(-1)n+1×
.
=(1-2)(1+2)+(3-4)(3+4)+…+(9-10)(9+10)
=-(1+2+3+…+10)
=-
| 10×11 |
| 2 |
=-55.
S27=12-22+32-42+…+252-262+272
=(1-2)(1+2)+(3-4)(3+4)+…+(25-26)(25+26)+272
=-(1+2+3+…+26)+272
=-
| 26(1+26) |
| 2 |
=378.
当n为偶数2k(k∈Z)时,
S2k═12-22+32-42+…+(2k-1)2-(2k)2
=(1-2)(1+2)+(3-4)(3+4)+…+(2k-1-2k)(2k-1+2k)
=-(1+2+…+2k-1+2k)
=-
| 2k(1+2k) |
| 2 |
=-
| n(1+n) |
| 2 |
当n为奇数2k-1(k∈Z)时,
S2k-1=S2k-(-1)2k+1(2k)2
=-
| (n+1)(n+2) |
| 2 |
=
| n(n+1) |
| 2 |
综上可得:Sn=(-1)n+1×
| n(n+1) |
| 2 |
故答案分别为:-55;378;(-1)n+1×
| n(n+1) |
| 2 |
点评:本题考查了等差数列的前n项和公式、平方差公式,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
函数f(x)=x-ex在R上的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |
 ,则
,则 的取值范围是( )
的取值范围是( )



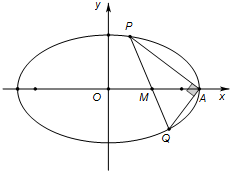 已知椭圆C:
已知椭圆C: