题目内容
设h是一个正整数,证明(1+h)n≥1+nh,n是任意正整数.
考点:数学归纳法
专题:点列、递归数列与数学归纳法,推理和证明
分析:要证明(1+h)n≥1+nh,先证明n=1时,(1+h)n≥1+nh成立,再假设n=k时,(1+h)n≥1+nh成立,进而证明出n=k+1时,(1+h)n≥1+nh也成立,即可得到对于任意正整数n:(1+h)n≥1+nh.
解答:
证明:将(1+h)n≥1+nh看成关于n的不等式,h为参数,以下用数学归纳法证明:
(ⅰ)当n=1时,原不等式成立;
当n=2时,左边=1+2h+h2,右边=1+2h,
因为h2≥0,所以左边≥右边,原不等式成立;
(ⅱ)假设当n=k时,不等式成立,即(1+h)k≥1+kh,
则当n=k+1时,
∵h是一个正整数,
∴1+h>0,于是在不等式(1+h)k≥1+kh两边同乘以1+h得
(1+h)k•(1+h)≥(1+kh)•(1+h)=1+(k+1)h+kh2≥1+(k+1)h,
所以(1+h)k+1≥1+(k+1)h.即当n=k+1时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数n,不等式都成立.
(ⅰ)当n=1时,原不等式成立;
当n=2时,左边=1+2h+h2,右边=1+2h,
因为h2≥0,所以左边≥右边,原不等式成立;
(ⅱ)假设当n=k时,不等式成立,即(1+h)k≥1+kh,
则当n=k+1时,
∵h是一个正整数,
∴1+h>0,于是在不等式(1+h)k≥1+kh两边同乘以1+h得
(1+h)k•(1+h)≥(1+kh)•(1+h)=1+(k+1)h+kh2≥1+(k+1)h,
所以(1+h)k+1≥1+(k+1)h.即当n=k+1时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数n,不等式都成立.
点评:数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立

练习册系列答案
相关题目
 是定义在区间
是定义在区间 上的奇函数,则
上的奇函数,则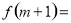 ( )
( ) 一个正三菱柱的左视图是边长为2
一个正三菱柱的左视图是边长为2 在平面直角坐标系xOy中,椭圆
在平面直角坐标系xOy中,椭圆