题目内容
某人在草地上散步，他看到正西方向有两根相距6m的标杆，当他向正北方向步行3min后，看到一根标杆在其西南方向上，另一根标杆在其南偏西30°方向上，求此人步行的速度（精确到0.1m/min）．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：设该船的位置是从B到A，两个灯塔位置分别为C、D，如图所示AB⊥BD，∠BAD=45°，∠BAC=30°，利用正切函数建立方程，即可求此人步行的速度．
解答：
解：如图，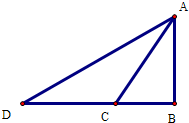
设该人的位置是从B到A，两个灯塔位置分别为C、D
依题意有AB⊥BD，∠BAD=45°，∠BAC=30°，
设此人步行的速度为xm/min，则
tan30°=
从而x=
=
+1≈2.7m/min
设该人的位置是从B到A，两个灯塔位置分别为C、D依题意有AB⊥BD，∠BAD=45°，∠BAC=30°，
设此人步行的速度为xm/min，则
tan30°=
| 3x |
| 3x+6 |
从而x=
| 2 | ||
|
| 3 |
点评：本题给出实际应用问题，求此人步行的速度．着重考查了解直角三角形和方位角等概念，属于基础题．
练习册系列答案
相关题目
如图，已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，底面△ABC中AC=3，AB=5，BC=4，点D是AB的中点，求证：（1）AC⊥BC1；
函数f（x）=Asin（ωx+φ）（其中ω＞0，A＞0，|φ|＜