题目内容
函数f(x)=x-ex在R上的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:根据导数判断得出函数f(x)=x-ex,在(-∞,0)单调递增,(0,+∞)单调递减,求出x=0时,f(x)max=f(0)=0-1=-1<0,判断得出函数无零点.
解答:
解:∵函数f(x)=x-ex,
∴f′(x)=1-ex,
f′(x)=1-ex=0,x=0,
f′(x)=1-ex>0,x<0,
f′(x)=1-ex<0,x>0,
即函数f(x)=x-ex,在(-∞,0)单调递增,(0,+∞)单调递减,
x=0时,f(x)max=f(0)=0-1=-1<0,
故函数f(x)=x-ex在R上的零点个数为0,
故选:A.
∴f′(x)=1-ex,
f′(x)=1-ex=0,x=0,
f′(x)=1-ex>0,x<0,
f′(x)=1-ex<0,x>0,
即函数f(x)=x-ex,在(-∞,0)单调递增,(0,+∞)单调递减,
x=0时,f(x)max=f(0)=0-1=-1<0,
故函数f(x)=x-ex在R上的零点个数为0,
故选:A.
点评:本题考查了函数的导数在判断函数单调性的运用,结合函数函数最值判断函数零点个数,属于中档题.

练习册系列答案
相关题目
根据表格中的数据,可以断定函数f(x)=ex-x-2的一个零点所在的区间是( )
| x+2 | 1 | 2 | 3 | 4 | 5 |
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| A、(-1,0) |
| B、(1,2) |
| C、(0,1) |
| D、(2,3) |
 ,则实数
,则实数 的值等于 .
的值等于 .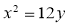 的焦点为
的焦点为 ,经过点
,经过点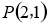 的直线
的直线 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为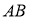 的中点,则
的中点,则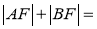 .
. 如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1;
如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1; 一个正三菱柱的左视图是边长为2
一个正三菱柱的左视图是边长为2 如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设
如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设