题目内容
已知
,
满足|
|=5,|
|≤1,且|
-4
|≤
,则
•
的最小值为 .
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:
,
满足|
|=5,|
|≤1,且|
-4
|≤
,利用数量积运算性质、绝对值不等式的性质可得:
2-8
•
+16
2≤21,5-4|
|≤
,化简即可得出.
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
| a |
| a |
| b |
| b |
| b |
| 21 |
解答:
解:∵
,
满足|
|=5,|
|≤1,且|
-4
|≤
,
∴
2-8
•
+16
2≤21,5-4|
|≤
,
化为
•
≥
,|
|≥
,即|4
2|≥
.
∴
•
≥
,
故答案为:
.
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
∴
| a |
| a |
| b |
| b |
| b |
| 21 |
化为
| a |
| b |
1+4
| ||
| 2 |
| b |
5-
| ||
| 4 |
| b |
23-5
| ||
| 2 |
∴
| a |
| b |
25-5
| ||
| 4 |
故答案为:
25-5
| ||
| 4 |
点评:本题考查了数量积运算性质、绝对值不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
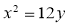 的焦点为
的焦点为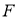 ,经过点
,经过点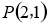 的直线
的直线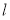 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为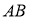 的中点,则
的中点,则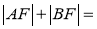 .
. 一个正三菱柱的左视图是边长为2
一个正三菱柱的左视图是边长为2 在平面直角坐标系xOy中,椭圆
在平面直角坐标系xOy中,椭圆 如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设
如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设