题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
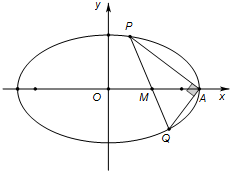
(Ⅱ) 如图,设A是椭圆长轴一个顶点,直线l与椭圆交于P、Q(不同于A),若∠PAQ=90°,求证直线l恒过x轴上的一个定点,并求出这个定点的坐标.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(I)由题意可得:
=
,2a=4,b2=a2-c2即可得出;
(II)设直线AP的方程为l1:y=k(x-2),P(x1,y1)与椭圆的方程联立可得P,同理可得Q,设直线PQ交x轴于点M(m,0),利用
∥
,即可得出.
| c |
| a |
| ||
| 2 |
(II)设直线AP的方程为l1:y=k(x-2),P(x1,y1)与椭圆的方程联立可得P,同理可得Q,设直线PQ交x轴于点M(m,0),利用
| MP |
| MQ |
解答:
解:(Ⅰ)2a=4,a=2,
=
,c=
,b=
=1,
∴椭圆的方程是
+y2=1.
(Ⅱ)设直线AP的方程为l1:y=k(x-2),P(x1,y1)
由
得,(1+4k2)x2-16k2x+16k2-4=0.
则2•x1=
,
∴x1=
,y1=k(x1-2)=-
,
∵∠PAQ=90°,设Q(x2,y2)
以-
代换x1,y1表达式中的k,得x2=
,y2=
,
设直线PQ交x轴于点M(m,0),
∥
,
=(
-m,-
),
=(
-m,
),
∴(
-m)•
-(
-m)•(-
)=0,
5m(1+k2)=6(1+k2)则m=
,
∴直线EF过定点(
,0).
| c |
| a |
| ||
| 2 |
| 3 |
| a2-c2 |
∴椭圆的方程是
| x2 |
| 4 |
(Ⅱ)设直线AP的方程为l1:y=k(x-2),P(x1,y1)
由
|
则2•x1=
| 16k2-4 |
| 1+4k2 |
∴x1=
| 8k2-2 |
| 1+4k2 |
| 4k |
| 4k2+1 |
∵∠PAQ=90°,设Q(x2,y2)
以-
| 1 |
| k |
| 8-2k2 |
| 4+k2 |
| 4k |
| 4+k2 |
设直线PQ交x轴于点M(m,0),
| MP |
| MQ |
| MP |
| 8k2-2 |
| 4k2+1 |
| 4k |
| 4k2+1 |
| MQ |
| 8-2k2 |
| 4+k2 |
| 4k |
| 4+k2 |
∴(
| 8k2-2 |
| 4k2+1 |
| 4k |
| 4+k2 |
| 8-2k2 |
| 4+k2 |
| 4k |
| 4k2+1 |
5m(1+k2)=6(1+k2)则m=
| 6 |
| 5 |
∴直线EF过定点(
| 6 |
| 5 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得交点、相互垂直的直线斜率之间的关系、共线向量定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
根据表格中的数据,可以断定函数f(x)=ex-x-2的一个零点所在的区间是( )
| x+2 | 1 | 2 | 3 | 4 | 5 |
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| A、(-1,0) |
| B、(1,2) |
| C、(0,1) |
| D、(2,3) |
 ,则函数
,则函数 的奇偶性为__________
的奇偶性为__________ 如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1;
如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1; 一个正三菱柱的左视图是边长为2
一个正三菱柱的左视图是边长为2