题目内容
x2+ax+1≥0对x∈R恒成立,求a的取值范围.
考点:函数恒成立问题,一元二次不等式的解法
专题:函数的性质及应用
分析:把f(x)≥0对x∈R恒成立,转化为x2-ax+1≥0对x∈R恒成立,利用一元二次不等式的解法,可判断∴△=a2-4≤0,就可得到a的范围.
解答:
解:x2+ax+1≥0对x∈R恒成立,
∴△=a2-4≤0,解得,-2≤a≤2.
∴a的取值范围[-2,2]
∴△=a2-4≤0,解得,-2≤a≤2.
∴a的取值范围[-2,2]
点评:本题考查函数恒成立,二次函数与一元二次不等式的解法,以及直接法求函数的值域,属于函数的常规题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若F(
)=x,则下列等式正确的是( )
| 1-x |
| 1+x |
| A、F(2-x)=1-F(x) | ||
B、F(-x)=
| ||
| C、F(x-1)=F(x) | ||
| D、F(F(x))=-x |
椭圆:
+
=1上的一点A关于原点的对称点为B,F2为它的右焦点,若AF2⊥BF2,则三角形△AF2B的面积是( )
| x2 |
| 25 |
| y2 |
| 9 |
A、
| ||
| B、10 | ||
| C、6 | ||
| D、9 |
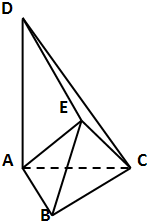 如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2
如图所示,△ABC和△BCE是边长为2的正三角形,且平面ABC⊥平面BCE,AD⊥平面ABC,AD=2