题目内容
15.有下列三种说法:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②“p∨q为真”是“¬p为假”的必要不充分条件;
③在区间[0,π]上随机取一个数x,则事件“sinx≥$\frac{1}{2}$”发生的概率是$\frac{5}{6}$.
其中正确说法的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①根据含有量词的命题的否定进行判断.
②根据复合命题的真假关系以及充分条件和必要条件的定义进行判断.
③根据几何概型的概率公式进行计算.
解答 解:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;正确,
②当p假q真时,满足p∨q为真,但¬p为假不成立,即充分性不成立,
若¬p为假,则p为真命题.则p∨q为真,即必要性成立,即②“p∨q为真”是“¬p为假”的必要不充分条件;正确;
③在区间[0,π]上,由sinx≥$\frac{1}{2}$,得$\frac{π}{6}$≤x≤$\frac{5π}{6}$,
则对应的概率P=$\frac{\frac{5π}{6}-\frac{π}{6}}{π}$═$\frac{2}{3}$,则在区间[0,π]上随机取一个数x,则事件“sinx≥$\frac{1}{2}$”发生的概率是$\frac{5}{6}$,错误.
故选:C
点评 本题主要考查命题的真假判断,涉及含有量词的命题的否定,充分条件和必要条件的判断以及几何概型的概率计算,涉及的知识点较多,但难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,若抛物线的准线交双曲线于A、B两点,当|AB|=4a时,此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
20.已知△ABC的内切圆与边AB,AC,BC相切于点P,Q,R,若|CR|=1,|AB|=2,则动点C的轨迹曲线的离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 ,点
,点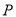 是
是 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点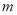 .
.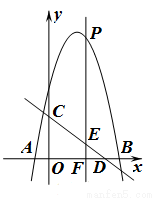
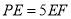 ,求
,求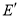 是点
是点 关于直线
关于直线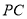 的对称点、是否存在点
的对称点、是否存在点 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点