题目内容
18.已知实数x,y满足$\left\{\begin{array}{l}{y≥1}\\{y≤2x-1}\\{x+y≤8}\end{array}\right.$,则z=x+y的最小值为2.分析 画出满足条件的平面区域,求出角点的坐标,结合函数图象求出z的最小值即可.
解答  解:画出满足条件的平面区域,如图示:,
解:画出满足条件的平面区域,如图示:,
由$\left\{\begin{array}{l}{y=1}\\{y=2x-1}\end{array}\right.$,解得B(1,1),
由z=x+y得:y=-x+z,
显然直线过B时z最小,
z的最小值是2,
故答案为:2.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知某工程在很大程度上受当地年降水量的影响,施工期间的年降水量X(单位:mm)对工期延误天数Y的影响及相应的概率P如表所示:
在降水量X至少是100的条件下,工期延误不超过15天的概率为( )
| 降水量X | X<100 | 100≤X<200 | 200≤X<300 | X≥300 |
| 工期延误天数Y | 0 | 5 | 15 | 30 |
| 概率P | 0.4 | 0.2 | 0.1 | 0.3 |
| A. | 0.1 | B. | 0.3 | C. | 0.42 | D. | 0.5 |
10.己知集合A={x|2x≥1},B={x|x2-3x+2≥0},则A∩B=( )
| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x<或x≥2} |
13.若x,2x+1,4x+5是等比数列{an}的前三项,则an等于( )
| A. | 2n-1 | B. | 3n-1 | C. | 2n | D. | 3n |
10.已知α,β是空间中两个不同的平面,m为平面β内的一条直线,则“α⊥β”是“m⊥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 ,点
,点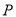 是
是 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点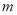 .
.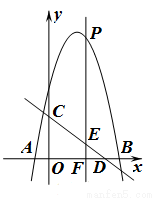
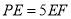 ,求
,求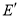 是点
是点 关于直线
关于直线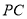 的对称点、是否存在点
的对称点、是否存在点 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点