题目内容
18.已知集合A={x|y=x2+1},B={y|y=x2+1},则下列关系正确的是( )| A. | A∩B=∅ | B. | A∩B=A | C. | A=B | D. | A∩B=B |
分析 求解一元二次函数的定义域化简集合A,求解值域化简集合B,再逐一判断则答案可求.
解答 解:集合A={x|y=x2+1}=R,B={y|y=x2+1}=[1,+∞),
则A∩B=B,故A,B不正确,则A≠B,故C不正确,
则A∩B=B,故D正确.
故选:D.
点评 本题考查了集合的包含关系判断及应用,考查了函数的定义域和值域的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知某工程在很大程度上受当地年降水量的影响,施工期间的年降水量X(单位:mm)对工期延误天数Y的影响及相应的概率P如表所示:
在降水量X至少是100的条件下,工期延误不超过15天的概率为( )
| 降水量X | X<100 | 100≤X<200 | 200≤X<300 | X≥300 |
| 工期延误天数Y | 0 | 5 | 15 | 30 |
| 概率P | 0.4 | 0.2 | 0.1 | 0.3 |
| A. | 0.1 | B. | 0.3 | C. | 0.42 | D. | 0.5 |
6.某单位从包括甲、乙在内的5名应聘者中招聘2人,如果这5名应聘者被录用的机会均等,则甲、乙两人中至少有1人被录用的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
3.已知0<θ<$\frac{π}{2}$,f(θ)=1+m+m($\frac{cosθ-1}{sinθ}$)+$\frac{sinθ-1}{cosθ}$(m>0),则使得f(θ)有最大值时的m的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
10.己知集合A={x|2x≥1},B={x|x2-3x+2≥0},则A∩B=( )
| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x<或x≥2} |
 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 ,点
,点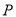 是
是 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点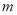 .
.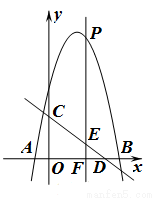
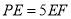 ,求
,求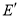 是点
是点 关于直线
关于直线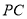 的对称点、是否存在点
的对称点、是否存在点 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点