一抛物线形拱桥.当水面宽4米时.水面离拱顶2米.若水面下降1米.则水面的宽为( )A．$\sqrt{6}$米B．2$\sqrt{6}$米C．6米D．8米题目和参考答案——青夏教育精英家教网—

题目内容

17．一抛物线形拱桥，当水面宽4米时，水面离拱顶2米，若水面下降1米，则水面的宽为（　　）

A．

$\sqrt{6}$米

B．

2$\sqrt{6}$米

C．

6米

D．

8米

分析先建立直角坐标系，将A点代入抛物线方程求得m，得到抛物线方程，再把y=-3代入抛物线方程求得x₀进而得到答案．

解答解：如图建立直角坐标系，设抛物线方程为x²=my，
将A（2，-2）代入x²=my，
得m=-2
∴x²=-2y，代入B（x₀，-3）得x₀=$\sqrt{6}$，
故水面宽为2$\sqrt{6}$米．
故选：B

点评本题主要考查抛物线的应用．考查了学生利用抛物线解决实际问题的能力．属于中档题．

练习册系列答案

8．

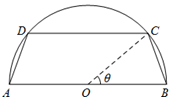一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分，现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，C，D在半圆上），设∠BOC=θ，直四棱柱木梁的体积为V（单位：m³），侧面积为S（单位：m²）．
（Ⅰ）分别求V与S关于θ的函数表达式；
（Ⅱ）求侧面积S的最大值；
（Ⅲ）求θ的值，使体积V最大．

5．已知x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x-2y+2≤0\\ y≤2\end{array}\right.$，则z=2x-3y的最小值为（　　）

12．

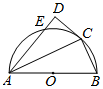已知AB为半圆O的直径，C为半圆上一点，CD是半圆的切线，AC平分∠BAD，AD交半圆于点E．
（Ⅰ）求证：AD⊥CD；
（Ⅱ）若AB=5，DE=1，求AE的长．

2．已知命题p：函数f（x）=lg（x²+mx+m）的定义域为R，命题q：函数g（x）=x²-2x-1在[m，+∞）上是增函数．
（Ⅰ）若p为真，求m的范围；
（Ⅱ）若“p∨q”为真命题，“p∧q”为假命题，求m的取值范围．

9．“x²-4x＜0”的一个充分不必要条件为（　　）

6．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x+y≥-1}\\{x-y≤-1}\\{2x-3y≥-6}\end{array}\right.$
（1）求目标函数z=2x-y的取值范围；
（2）求目标函数z=x²+y²的最大值．

7．已知a∈{0，1，2}，b∈{-1，1，3，5}，则函数f（x）=ax²-2bx在区间（1，+∞）上为增函数的概率是（　　）

试题分类