题目内容
7.已知{an}是等差数列,a1=2,公差d≠0,Sn为其前n项和,若a1、a2、a5成等比数列,则S5=50.分析 由题意设等差数列{an}的公差为d,由a1,a2,a5成等比数列可得d的方程,解得d代入等差数列的求和公式可得.
解答 解:由题意设等差数列{an}的公差为d,d≠0,
∵a1,a2,a5成等比数列,
∴a22=a1•a5,
∴(2+d)2=2(2+4d),
解得d=4,或d=0(舍去)
∴S5=5a1+$\frac{5×4}{2}$d=5×2+10×4=50.
故答案为:50.
点评 本题考查等差数列的通项公式和求和公式,同时考查等比数列的中项性质,求出数列的公差是解决的关键,属中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
15.函数f(x)=ax+$\frac{1}{a}$(2-x),其中a>0,记f(x)在区间[0,2]上的最小值为g(a),则函数g(a)的最大值为( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
2. 如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )
如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )
 如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )
如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
17.已知函数g(x)是R上的偶函数,当x<0时,g(x)=ln(1-x),函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ g(x),x>0\end{array}\right.$满足f(2-x2)>f(x),则实数x的取值范围是( )
| A. | (-∞,1)∪(2,+∞) | B. | (-∞,-2)∪(1,+∞) | C. | (1,2) | D. | (-2,1) |
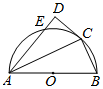 已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.
已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.