题目内容
20.已知函数f(x)=3x-$\frac{1}{{{3^{|x|}}}}$.(1)若f(x)=0,求x的取值集合;
(2)若对于t∈[1,3]时,不等式3tf(2t)+mf(t)≥0恒成立,求实数m的取值范围.
分析 (1)f(x)=3x-$\frac{1}{{{3^{|x|}}}}$,分x<0与x≥0讨论,由f(x)=0,即可求得x的取值集合;
(2)当t∈[1,3]时,f(t)=3t-$\frac{1}{{3}^{t}}$>0,于是不等式3tf(2t)+mf(t)≥0恒成立可化为m≥-32t-1恒成立,利用指数函数的单调性即可求得实数m的取值范围.
解答 解:(1)当x<0时,f(x)=3x-3x=0恒成立;
当x≥0时,f(x)=3x-$\frac{1}{{3}^{x}}$=0,解得:x=0;
综上所述,x的取值集合为{x|x≤0}.
(2)∵t∈[1,3],∴f(t)=3t-$\frac{1}{{3}^{t}}$>0.
∴3tf(2t)+mf(t)≥0恒成立可化为:
3t(32t-$\frac{1}{{3}^{2t}}$)+m(3t-$\frac{1}{{3}^{t}}$)≥0恒成立,
即3t(3t+$\frac{1}{{3}^{t}}$>)+m≥0,即m≥-32t-1恒成立.
令g(t)=-32t-1,则g(t)在[1,3]上递减,∴g(x)max=g(1)=-10.
∴所求实数m的取值范围是[-10,+∞).
点评 本题考查函数恒成立问题,考查等价转化思想与函数方程思想的综合运用,突出指数函数单调性与分离参数法的应用,属于难题.

练习册系列答案
相关题目
10.函数f(x)=x2-(2a-1)x-3在$({\frac{3}{2},+∞})$上是增函数,则实数a的范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≤2 | D. | a≥2 |
15.函数f(x)=ax+$\frac{1}{a}$(2-x),其中a>0,记f(x)在区间[0,2]上的最小值为g(a),则函数g(a)的最大值为( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
5.已知x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x-2y+2≤0\\ y≤2\end{array}\right.$,则z=2x-3y的最小值为( )
| A. | -6 | B. | -4 | C. | -3 | D. | -2 |
9.“x2-4x<0”的一个充分不必要条件为( )
| A. | 0<x<4 | B. | 0<x<2 | C. | x>0 | D. | x<4 |
10.已知复数$z=\frac{1}{1+i}+i$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
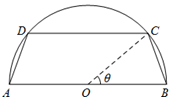 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).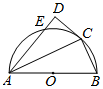 已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.
已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.