题目内容
4.i为虚数单位,z=$\frac{1}{cos2θ-isin2θ}$对应的点在第二象限,则θ是第一、三象限的角.分析 利用共轭复数的意义可得z=$\frac{1}{cos2θ-isin2θ}$=cos2θ+isin2θ对应的点在第二象限,可得cos2θ<0,sin2θ>0,解出θ即可得出结论.
解答 解:z=$\frac{1}{cos2θ-isin2θ}$=$\frac{cos2θ+isin2θ}{(cos2θ-isin2θ)(cos2θ+isin2θ)}$=cos2θ+isin2θ对应的点在第二象限,
∴cos2θ<0,sin2θ>0,
∴$2kπ+\frac{π}{2}$<2θ<2kπ+π,k∈Z.
解得kπ+$\frac{π}{4}$<θ<kπ+$\frac{π}{2}$,k∈Z.
k=2n(n∈Z)时,2nπ+$\frac{π}{4}$<θ<2nπ+$\frac{π}{2}$,θ为第一象限角.
k=2n-1(n∈Z)时,2nπ-$\frac{3π}{4}$<θ<2nπ-$\frac{π}{2}$,θ为第三象限角.
综上可得:θ是第一、三象限的角.
故答案为:一、三.
点评 本题考查了复数的运算法则、几何意义、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.设f(x)=$\left\{\begin{array}{l}{1-\sqrt{x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,则f(f(-log23))=( )
| A. | $\frac{3-\sqrt{3}}{3}$ | B. | $\frac{3}{2}$ | C. | 1-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
12.已知等差数列{an}的公差d=2,a3=5,数列{bn},bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,则数列{bn}的前10项的和为( )
| A. | $\frac{10}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{19}$ | D. | $\frac{20}{19}$ |
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )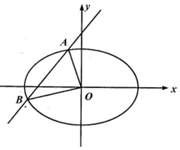 如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.
如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.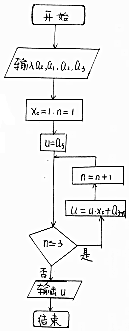 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )