题目内容
13.设集合A={x|y=2x+3},B={(x,y)|y=4x+1},则A∩B=∅.分析 根据求出集合A,由直线方程判断出集合B,由交集的运算求出A∩B.
解答 解:由题意知,集合A={x|y=2x+3}=R,
B={(x,y)|y=4x+1}是直线y=4x+1上所有的点构成的集合,
则A∩B=∅,
故答案为:∅.
点评 本题考查交集及其运算,以及集合的表示方法:描述法,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.函数f(x)为区间(-∞,0)∪(0,+∞)上的奇函数,且(0,+∞)为增区间,若f(-1)=0,则当$\frac{f(x)}{x}$<0时,x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
5.直线l与平面α有公共点,则有( )
| A. | l∥α | B. | l?α | C. | l与α相交 | D. | l?α或l与α相交 |
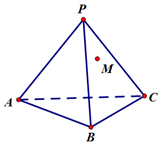 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3