题目内容
19. 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设D1在平面ABC的射影为E,连接D1E,根据线面垂直的性质与判定,面面垂直的判定定理寻找互相垂直的平面.
解答 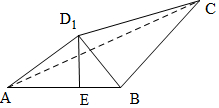 解:设D1在平面ABC的射影为E,连接D1E,则D1E⊥平面ABC,
解:设D1在平面ABC的射影为E,连接D1E,则D1E⊥平面ABC,
∵D1E?平面ABD1,∴平面ABD1⊥平面ABC.
∵D1E⊥平面ABC,BC?平面ABC,
∴D1E⊥BC,又AB⊥BC,D1E∩AB=E,
∴BC⊥平面ABD1,又BC?平面BCD1,
∴平面BCD1⊥平面ABD1,
∵平面BC⊥平面ABD1,AD1?平面ABD1,
∴BC⊥AD1,又CD1⊥AD1,BC∩CD1=C,
∴AD1⊥平面BCD1,又AD1?平面ACD1,
∴平面ACD1⊥平面BCD1.
∴共有3对平面互相垂直.
故选:B.
点评 本题考查了线面垂直的性质与判定,面面垂直的判定,属于中档题.

练习册系列答案
相关题目
7.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了有圆锥的底面周长L与高,计算其体积V的近似公式V≈$\frac{1}{48}$L2h,它实际上是将圆锥体积公式中的圆周率π近似取为4,那么近似公式V≈$\frac{1}{75}$L2h相当于将圆锥体积公式中π的近似取为( )
| A. | $\frac{25}{6}$ | B. | $\frac{25}{8}$ | C. | $\frac{25}{3}$ | D. | $\frac{25}{4}$ |
7.关于x的方程x2-x•cosA•cosB-cos2$\frac{C}{2}$=0有一个根为1,则△ABC一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
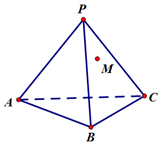 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3