题目内容

14．已知平面向量$\overrightarrow a=（1，2）$，$\overrightarrow b=（m，-4）$，且$\overrightarrow a∥\overrightarrow b$，则$\overrightarrow a•\overrightarrow b$=（　　）
A．4B．-6C．-10D．10

分析 先根据向量的共线求出m的值，再根据向量的数量积求出即可

解答 解：平面向量$\overrightarrow a=（1，2）$，$\overrightarrow b=（m，-4）$，且$\overrightarrow a∥\overrightarrow b$，
∴1×（-4）=2m，
解得m=-2，
则$\overrightarrow a•\overrightarrow b$=1×（-2）+2×（-4）=-10，
故选：C

点评 本题考查了向量的坐标运算和向量的共线和向量的数量积公式，属于基础题

练习册系列答案
相关题目
4．已知集合A={x|2x＞1}，B={x|log2x＜0}，则∁AB=（　　）
A．（0，1）B．（0，1]C．（1，+∞）D．[1，+∞）
5．已知△ABC中，角A，B，C所对的边分别是a，b，c，且acosA=bcosB，则该三角形的形状是等腰三角形或直角三角形．
2．已知文具盒中有5支铅笔，其中3支红色，2支黄色．现从这5只铅笔中任取2支，这两支铅笔颜色恰好不同的概率为（　　）
A．0.4B．0.6C．0.8D．1
9．设复数z=2+i，则|z-$\overline{z}$|=（　　）
A．4B．0C．2D．$2\sqrt{10}$
19．执行如图所示的程序框图，若m=8，则输出的结果是（　　）
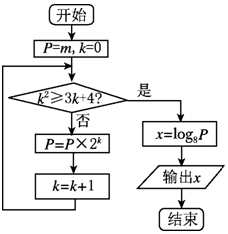
A．2B．$\frac{7}{3}$C．3D．$\frac{13}{3}$
6．已知函数f（x）=$\frac{{4}^{x}-{4}^{-x}}{3}$+log3（$\sqrt{{x}^{2}+1}$+x），那么关于x的不等式f（2x-6）+f（x）＞0的解集为（　　）
A．{x|x＞-2}B．{x|x＞2}C．{x|0＜x＜2}D．{x|-2＜x＜2}
3．在长方体ABCD-A1B1C1D1的十二条棱中，与面对角线AC垂直且异面的棱的条数是（　　）
A．2B．4C．6D．8
4．在平面直角坐标系xOy中，已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$（φ为参数），以原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=sinθ．
（Ⅰ）求曲线C1的极坐标方程及曲线C2的直角坐标方程；
（Ⅱ）已知曲线C1，C2交于O，A两点，过O点且垂直于OA的直线与曲线C1，C2交于M，N两点，求|MN|的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网