题目内容
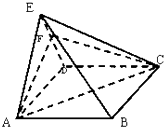 如图,在四棱锥E-ABCD中,底面ABCD为边长为5的正方形,AE⊥平面CDE,AE=3.
如图,在四棱锥E-ABCD中,底面ABCD为边长为5的正方形,AE⊥平面CDE,AE=3.(1)若F为DE的中点,求证:BE∥平面ACF;
(2)求直线BE与平面ABCD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结AC,BD交于O,连OF,利用三角形中位线的性质,证明OF∥BE,利用线面平行的判定证明BE∥平面ACF;
(2)证明EH⊥平面ABCD,可得BH为BE在平面ABCD内的射影,∠EBH为BE与平面ABCD的所成角的平面角,从而可求直线BE与平面ABCD所成角的正弦值.
(2)证明EH⊥平面ABCD,可得BH为BE在平面ABCD内的射影,∠EBH为BE与平面ABCD的所成角的平面角,从而可求直线BE与平面ABCD所成角的正弦值.
解答:
(1)证明:连结AC,BD交于O,连OF.
∵F为DE中点,O为BD中点,
∴OF∥BE,
∵OF?平面ACF,BE?平面ACF,
∴BE∥平面ACF.…(6分)
(2)解:过E作EH⊥AD于H,连结BH,…(7分)
∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,
∵EH?平面DAE,
∴CD⊥EH,
∵CD∩AD=D,CD,AD?平面ABCD,
∴EH⊥平面ABCD,
∴BH为BE在平面ABCD内的射影,
∴∠EBH为BE与平面ABCD的所成角的平面角,
又∵CD∥AB,∴AB⊥平面DAE,
∴△ABE为直角三角形,
∴BE=
,且HE=
,
∴sin∠EBH=
.…(12分)
∵F为DE中点,O为BD中点,
∴OF∥BE,
∵OF?平面ACF,BE?平面ACF,
∴BE∥平面ACF.…(6分)
(2)解:过E作EH⊥AD于H,连结BH,…(7分)
∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,
∵EH?平面DAE,
∴CD⊥EH,
∵CD∩AD=D,CD,AD?平面ABCD,
∴EH⊥平面ABCD,
∴BH为BE在平面ABCD内的射影,
∴∠EBH为BE与平面ABCD的所成角的平面角,
又∵CD∥AB,∴AB⊥平面DAE,
∴△ABE为直角三角形,
∴BE=
| 34 |
| 12 |
| 5 |
∴sin∠EBH=
6
| ||
| 85 |
点评:本题考查线面平行,考查线面垂直,考查线面角,正确运用线面平行的判定定理是关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
把1010(2)化为十进制数为( )
| A、20 | B、12 | C、10 | D、11 |
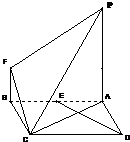 已知△ABC三内角A、B、C所对边的长分别为a、b、c,且3sin2A+3sin2B=4sinAsinB+3sin2C.
已知△ABC三内角A、B、C所对边的长分别为a、b、c,且3sin2A+3sin2B=4sinAsinB+3sin2C.