题目内容
(1)已知tanα=2,计算
的值;
(2)化简:
(3)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
| 4sinα-2cosα |
| 5cosα+3sinα |
(2)化简:
sin(π-α)cos(π+α)cos(
| ||
cos(3π-α)sin(3π+α)sin(
|
(3)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)将所求的关系式中的“弦”化“切”,代入计算即可;
(2)利用诱导公式化简即可;
(3)利用扇形的面积公式S=
lr计算即可.
(2)利用诱导公式化简即可;
(3)利用扇形的面积公式S=
| 1 |
| 2 |
解答:
解:(1)∵tanα=2,∴原式=
=
….(4分)
(2)原式=
=-tanα….(8分)
(3)设扇形的弧长为l,因为72°=72×
=
,
所以l=αr=
×20=8π(cm),所以S=
lr=
×8π×20=80π(cm2)….(12分)
| 4tanα-2 |
| 5+3tanα |
| 6 |
| 11 |
(2)原式=
| sinα(-cosα)sinα |
| (-cosα)(-sinα)cosα |
(3)设扇形的弧长为l,因为72°=72×
| π |
| 180 |
| 2π |
| 5 |
所以l=αr=
| 2π |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查同角三角函数基本关系的运用,考查运用诱导公式化简求值及扇形的面积公式的应用,属于中档题.

练习册系列答案
相关题目
已知数列{an}是公差不等于零的等差数列,若a1,ak,a2k(k∈N*且k≥2)是公比为q的等比数列,则公比q的最大值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
下列函数中是偶函数的是( )
| A、y=x3 |
| B、y=cosx |
| C、y=2x |
| D、y=lnx |
 将全体正偶数排成一个三角数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为
将全体正偶数排成一个三角数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为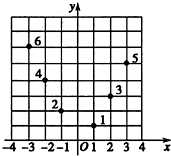 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示:
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示: