题目内容
已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且
•
=
•
.
(1)求动点P的轨迹C的方程;
(2)设M为直线l1:y=-m(m>2)上的任意一点,过点M作轨迹C的两条切线MA,MB.切点分别为A,B,试探究直线l1上是否存在点M,使得△MAB为直角三角形?若存在,有几个这样的点;若不存在,请说明理由.
| QP |
| QF |
| FP |
| FQ |
(1)求动点P的轨迹C的方程;
(2)设M为直线l1:y=-m(m>2)上的任意一点,过点M作轨迹C的两条切线MA,MB.切点分别为A,B,试探究直线l1上是否存在点M,使得△MAB为直角三角形?若存在,有几个这样的点;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题,平面向量数量积的运算,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)设动点P(x,y),则Q(x,-1),由
•
=
•
,可得
•(
+
)=0,利用数量积运算可得-x2+4y=0,即x2=4y.
(2)设A(x1,y1),B(x2,y2),M(x0,y0).由x2=4y,可得y′=
x,可得切线方程为:y=
x-
.又切线过点M,可得y0=
x0-
;同理可得过点B的切线方程为:y0=
x0-
.可知:x1,x2是方程y0=
x0-
的两个实数根.可得根与系数的关系:利用数量积运算可得
•
=x1x2-x0(x1+x2)+
+y1y2-y0(y1+y2)+
.可得:
•
=(m-1)(
+4m).当m>2时,
•
>0,∠AMB<
.利用斜率计算公式可得kMA•kAB=
,若kMA•kAB=-1,整理得(y0+2)
=-4.即(m-2)
=4,而m>2时,方程(m-2)
=4有解,即可得出.
| QP |
| QF |
| FP |
| FQ |
| QF |
| QP |
| FP |
(2)设A(x1,y1),B(x2,y2),M(x0,y0).由x2=4y,可得y′=
| 1 |
| 2 |
| x1 |
| 2 |
| ||
| 4 |
| x1 |
| 2 |
| ||
| 4 |
| x2 |
| 2 |
| ||
| 4 |
| x |
| 2 |
| x2 |
| 4 |
| MA |
| MB |
| x | 2 0 |
| y | 2 0 |
| MA |
| MB |
| x | 2 0 |
| MA |
| MB |
| π |
| 2 |
x0(x0±
| ||||
| 4 |
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
解答:
解:(1)设动点P(x,y),则Q(x,-1),
∵
•
=
•
,
∴
•(
+
)=0.
∵
=(-x,2),
=(0,y+1),
=(x,y-1),
∴(-x,2)•(x,2y)=0,
∴-x2+4y=0,即x2=4y.
(2)设A(x1,y1),B(x2,y2),M(x0,y0).
由x2=4y,可得y′=
x,
∴切点A的切线斜率为
x1,切线方程为:y-y1=
(x-x1),即y=
x-
.
又切线过点M,∴y0=
x0-
①,
同理可得过点B的切线方程为y=
x-
,又过点M,∴y0=
x0-
.②
由①②可知:x1,x2是方程y0=
x0-
的两个实数根.
∴x1+x2=2x0,x1x2=4y0.
•
=(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=x1x2-x0(x1+x2)+
+y1y2-y0(y1+y2)+
(*).
把x1+x2=2x0,x1x2=4y0.y1=
,y2=
代入(*)可得:
•
=4m2+m
-4m-
=(m-1)(
+4m).
当m>2时,
•
>0,∠AMB<
.
∵kAB=
=
=
=
.kMA=
=
,
∴kMA•kAB=
×
=
,
若kMA•kAB=-1,整理得(y0+2)
=-4.
∵y0=-m,∴(m-2)
=4,而m>2时,方程(m-2)
=4有解,
∴m>2时,MA⊥AB或MB⊥AB,△MAB为直角三角形.
即直线l1上存在两点M,使得△MAB为直角三角形.
∵
| QP |
| QF |
| FP |
| FQ |
∴
| QF |
| QP |
| FP |
∵
| QF |
| QP |
| FP |
∴(-x,2)•(x,2y)=0,
∴-x2+4y=0,即x2=4y.
(2)设A(x1,y1),B(x2,y2),M(x0,y0).
由x2=4y,可得y′=
| 1 |
| 2 |
∴切点A的切线斜率为
| 1 |
| 2 |
| x1 |
| 2 |
| x1 |
| 2 |
| ||
| 4 |
又切线过点M,∴y0=
| x1 |
| 2 |
| ||
| 4 |
同理可得过点B的切线方程为y=
| x2 |
| 2 |
| ||
| 4 |
| x2 |
| 2 |
| ||
| 4 |
由①②可知:x1,x2是方程y0=
| x |
| 2 |
| x2 |
| 4 |
∴x1+x2=2x0,x1x2=4y0.
| MA |
| MB |
| x | 2 0 |
| y | 2 0 |
把x1+x2=2x0,x1x2=4y0.y1=
| ||
| 4 |
| ||
| 4 |
| MA |
| MB |
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
当m>2时,
| MA |
| MB |
| π |
| 2 |
∵kAB=
| y1-y2 |
| x1-x2 |
| ||||||||
| x1-x2 |
| x1+x2 |
| 4 |
| x0 |
| 2 |
| x1 |
| 2 |
x0±
| ||||
| 2 |
∴kMA•kAB=
| x0 |
| 2 |
x0±
| ||||
| 2 |
x0(x0±
| ||||
| 4 |
若kMA•kAB=-1,整理得(y0+2)
| x | 2 0 |
∵y0=-m,∴(m-2)
| x | 2 0 |
| x | 2 0 |
∴m>2时,MA⊥AB或MB⊥AB,△MAB为直角三角形.
即直线l1上存在两点M,使得△MAB为直角三角形.
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线相切问题、一元二次方程的根与系数的关系、向量垂直与数量积的关系,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若椭圆的中心及两个焦点将两条准线之间的距离四等分,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
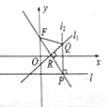 如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.
如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.