Question

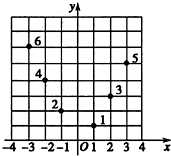如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{a_n}（n∈N^*）的前12项，如下表所示：

a1	a2	a3	a4	a5	a6	a7	a8	a9	a10	a11	a12
x1	y1	x2	y2	x3	y3	x4	y4	x5	y5	x6	y6

按如此规律下去，则a₂₀₁₁+a₂₀₁₂+a₂₀₁₃=

 

．

Answer 1

考点：归纳推理

专题：推理和证明

分析：由题意先求出对应数列{a_n}的前8项，再归纳出此数列的规律，利用规律求出式子的值．

解答： 解：由题意得，a₁=1，a₂=1，a₃=-1，a₄=2，a₅=2，a₆=3，a₇=-2，a₈=4，…，
这个数列的规律是奇数项为1，-1，2，-2，3，…；偶数项为1，2，3，…，
所以a₂₀₁₁+a₂₀₁₃=0，a₂₀₁₂=1 006，则a₂₀₁₁+a₂₀₁₂+a₂₀₁₃=1 006，
故答案为：1006．

点评：本题考查了归纳推理，难点在于发现其中的规律，考查观察、分析、归纳能力．