题目内容
7.已知双曲线的离心率为2,左右焦点分别为F1,F2,点A在双曲线上,若|F1A|=2|F2A|,∠AF2F1的正切值为$\sqrt{15}$.分析 由离心率公式,可得c=2a,根据双曲线的定义,以及余弦定理建立a,c的关系即可得到结论.
解答 解:∵双曲线C的离心率为2,
∴e=$\frac{c}{a}$=2,即c=2a,
由于点A在双曲线的右支上,则|F1A|-|F2A|=2a,
又|F1A|=2|F2A|,
∴解得|F1A|=4a,|F2A|=2a,|F1F2|=2c,
则由余弦定理得cos∠AF2F1=$\frac{4{a}^{2}+4{c}^{2}-16{a}^{2}}{2×2a×2c}$=$\frac{1}{4}$,
∴tan∠AF2F1=$\sqrt{15}$.
故答案为:$\sqrt{15}$.
点评 本题主要考查双曲线的定义和性质,利用离心率的定义和余弦定理是解决本题的关键,考查学生的计算能力.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
17.k>9是方程$\frac{x^2}{9-k}+\frac{y^2}{k-4}=1$表示双曲线的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
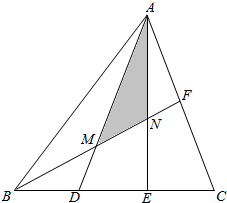 △ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.
△ABC中,D、E三等分BC,F为AC的中点,BF分别与AD、AE交于M、N.试求△AMN与△ABC面积之比.