题目内容
给出以下四个命题:
(1)若sinA=sinB,则△ABC为等腰三角形;
(2)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形;
(3)若tanAtanB>1,则△ABC一定是钝角三角形;
(4)△ABC中,a=2,b=3,C=60°,则三角形为锐角三角形.
以上正确命题的个数是 .
(1)若sinA=sinB,则△ABC为等腰三角形;
(2)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形;
(3)若tanAtanB>1,则△ABC一定是钝角三角形;
(4)△ABC中,a=2,b=3,C=60°,则三角形为锐角三角形.
以上正确命题的个数是
考点:命题的真假判断与应用
专题:解三角形,简易逻辑
分析:对于(1),在三角形内由角的正弦值相等得到角相等加以判断;
对于(2),由三角函数的有界性结合已知条件得到A=B=C;
对于(3),由tanAtanB>1得到tanAtanB>0,进一步得到cosAcosB>0,移项后结合两角和的余弦得答案;
对于(4),通过解三角形求出c,判断出最大角,再由余弦定理判断最大角为锐角得答案.
对于(2),由三角函数的有界性结合已知条件得到A=B=C;
对于(3),由tanAtanB>1得到tanAtanB>0,进一步得到cosAcosB>0,移项后结合两角和的余弦得答案;
对于(4),通过解三角形求出c,判断出最大角,再由余弦定理判断最大角为锐角得答案.
解答:
解:对于(1),若sinA=sinB,
∵0<A<π,0<B<π,0<A+B<π,
∴A=B,
△ABC为等腰三角形.命题(1)正确;
对于(2),若cos(A-B)cos(B-C)cos(C-A)=1,
∵-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1,
又-π<A-B<π,-π<B-C<π,-π<C-A<π,
∴cos(A-B)=1,cos(B-C)=1,cos(C-A)=1,
则A-B=0,B-C=0,C-A=0,故A=B=C,△ABC为正三角形.命题(2)正确;
对于(3),若tanAtanB>1,说明tanAtanB>0,
∵sinAsinB>0,
∴cosAcosB>0,这说明A和B同为锐角或者同为钝角,
又A和B均为三角形内角,
∴A、B同为锐角,由此有sinAsinB>cosAcosB,
∴cosAcosB-sinAsinB<0,即cos(A+B)<0,
∴
<A+B<π,由此C<
.
因此△ABC一定是锐角三角形.命题(3)错误;
对于(4),若a=2,b=3,C=60°,
根据余弦定理,得c2=22+32-2×2×3cos60°=7.
∴c=
,可得a<c<b,
∴A<C<B,因此B是△ABC中的最大角,
∵cosB=
=
>0,而B∈(0,π),
∴B是锐角,从而A、C均为锐角,
∴△ABC为锐角三角形.命题(4)正确.
∴正确命题的个数是3个.
故答案为:3.
∵0<A<π,0<B<π,0<A+B<π,
∴A=B,
△ABC为等腰三角形.命题(1)正确;
对于(2),若cos(A-B)cos(B-C)cos(C-A)=1,
∵-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1,
又-π<A-B<π,-π<B-C<π,-π<C-A<π,
∴cos(A-B)=1,cos(B-C)=1,cos(C-A)=1,
则A-B=0,B-C=0,C-A=0,故A=B=C,△ABC为正三角形.命题(2)正确;
对于(3),若tanAtanB>1,说明tanAtanB>0,
∵sinAsinB>0,
∴cosAcosB>0,这说明A和B同为锐角或者同为钝角,
又A和B均为三角形内角,
∴A、B同为锐角,由此有sinAsinB>cosAcosB,
∴cosAcosB-sinAsinB<0,即cos(A+B)<0,
∴
| π |
| 2 |
| π |
| 2 |
因此△ABC一定是锐角三角形.命题(3)错误;
对于(4),若a=2,b=3,C=60°,
根据余弦定理,得c2=22+32-2×2×3cos60°=7.
∴c=
| 7 |
∴A<C<B,因此B是△ABC中的最大角,
∵cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 14 |
∴B是锐角,从而A、C均为锐角,
∴△ABC为锐角三角形.命题(4)正确.
∴正确命题的个数是3个.
故答案为:3.
点评:本题考查命题的真假判断与应用,考查了三角形形状的判定,训练了学生的逻辑思维能力,是中档题.

练习册系列答案
相关题目
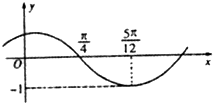 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

 在一次演讲比赛中,七位评委为某选手打出的分数的茎叶图(如图所示),去掉一个最高分一个最低分后,所剩数据的方差为
在一次演讲比赛中,七位评委为某选手打出的分数的茎叶图(如图所示),去掉一个最高分一个最低分后,所剩数据的方差为