题目内容
 在△ABC中,已知∠BAC=α,AB=c,AC=b,如图建立直角坐标系,利用两点间的距离公式计算BC2,并由此证明余弦定理.
在△ABC中,已知∠BAC=α,AB=c,AC=b,如图建立直角坐标系,利用两点间的距离公式计算BC2,并由此证明余弦定理.考点:余弦定理
专题:计算题,解三角形
分析:依题意,可求得B、C两点的坐标B(ccosα,csinα),C(b,0),利用两点间的距离公式可求得BC2,同理可证得余弦定理.
解答:
解:在△ABC中,∵∠BAC=α,AB=c,AC=b,
∴B(ccosα,csinα),C(b,0),
∴BC2=(ccosα-b)2+(csinα-0)2
=c2(cos2α+sin2α)-2bccosα+b2,
=c2+b2-2bccosα;
证明:在△ABC中,建立如图的直角坐标系,

则B(ccosA,csinA),C(b,0),
则a2=(ccosA-b)2+(csinA-0)2
=c2(cos2A+sin2A)-2bccosA+b2
=c2+b2-2bccosA,
即:a2=b2+c2-2bccosA;
同理可得,b2=a2+c2-2accosB,
c2=a2+b2-2abcosC.
∴B(ccosα,csinα),C(b,0),
∴BC2=(ccosα-b)2+(csinα-0)2
=c2(cos2α+sin2α)-2bccosα+b2,
=c2+b2-2bccosα;
证明:在△ABC中,建立如图的直角坐标系,

则B(ccosA,csinA),C(b,0),
则a2=(ccosA-b)2+(csinA-0)2
=c2(cos2A+sin2A)-2bccosA+b2
=c2+b2-2bccosA,
即:a2=b2+c2-2bccosA;
同理可得,b2=a2+c2-2accosB,
c2=a2+b2-2abcosC.
点评:本题考查余弦定理的证明,考查两点间距离公式的应用,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,已知角A=30°,a=8,b=8
,则△ABC的面积等于
( )
| 3 |
( )
A、32
| ||||
B、32
| ||||
C、32
| ||||
D、64
|

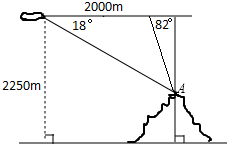 如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为
如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为