题目内容
已知f（x）=2sin（2x+
）+4．设A，B，C为△ABC的三个内角，且
=
，求f（x）在（0，B]上的值域．
| π |
| 3 |
| cosB |
| sinBcosC |
| 1 |
| 2sinA-sinC |
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：有等式关系利用两角和与差的三角函数求出B的余弦函数值，求出B的大小，然后利用正弦函数的值域求解函数的值域即可．
解答：
解：∵
=
，
∴2sinAcosB-cosBsinC=sinBcosC，
∴2sinAcosB=sin（B+C）=sin（π-A）=sinA，
∴cosB=
，
∴B=
．
x∈（0，
]，2x+
∈（
，π]，
∴sin（2x+
）∈[0，1]，
∴f（x）=2sin（2x+
）+4∈[4，5]．
f（x）在（0，B]上的值域为：[4，5]．
| cosB |
| sinBcosC |
| 1 |
| 2sinA-sinC |
∴2sinAcosB-cosBsinC=sinBcosC，
∴2sinAcosB=sin（B+C）=sin（π-A）=sinA，
∴cosB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
x∈（0，
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴sin（2x+
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
f（x）在（0，B]上的值域为：[4，5]．
点评：本题主要考查两角和与差的三角函数以及三角函数的化简，正弦函数的值域的求法，综合考查学生的运算能力．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
复数z=
的虚部为（ ）
| 2 |
| -1+i |
| A、-1 | B、-i | C、1 | D、i |
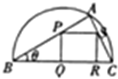如图所示，在直径为BC的半圆中，A是弧BC上一点，正方形PQRS内接于△ABC，若BC=a，∠ABC=θ，设△ABC的面积为Sl，正方形PQRS的面积为S2．
在△ABC中，已知∠BAC=α，AB=c，AC=b，如图建立直角坐标系，利用两点间的距离公式计算BC2，并由此证明余弦定理．