题目内容
设函数f(x)=(x-a)|x|+b.
(1)当a=2,b=3,求函数y=f(x)的零点;
(2)设b=-2,且对任意x∈[-1,1],f(x)<0恒成立,求实数a的取值范围.
(1)当a=2,b=3,求函数y=f(x)的零点;
(2)设b=-2,且对任意x∈[-1,1],f(x)<0恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数零点的判定定理
专题:函数的性质及应用
分析:(1)先将a=2,b=3代入,然后将函数化为分段函数,再根据二次函数的图象和性质,可得函数f(x)的图象,进而分析函数图象可得答案.
(2)将b=-2代入原式,f(x)<0可化为(x-a)|x|<2,再对x进行分类讨论分离参数a后,求函数最值即可.
(2)将b=-2代入原式,f(x)<0可化为(x-a)|x|<2,再对x进行分类讨论分离参数a后,求函数最值即可.
解答:
解(1)当a=2,b=3时
函数f(x)=(x-2)|x|+3的解析式可化为:
f(x)=
.
易知,当x≥0时,f(x)=(x-1)2+1≥1恒成立,故此时没有零点;当x<0时,令f(x)=0得x=-1或3(舍),故x=-1符合题意;
综上原函数的零点为-1.
(2)当b=-2时,由f(x)<0得,(x-a)|x|<2.
当x=0时,a取任意实数,不等式恒成立;
当0<x≤1时,原式可化为a>x-
,令g(x)=x-
,易知该函数在0<x≤1上单调递增,
∴a>gmax(x)=g(1)=-1;
当-1≤x<0时,原式可化为a>x+
.令g(x)=x+
,由g′(x)=1-
<0得-
<x<0或0<x<
.
故函数g(x)在[-1,0)上递减,所以此时a>g(x)max=g(-1)=-3.
综上,当a>-1时对任意x∈[-1,1],f(x)<0恒成立.
函数f(x)=(x-2)|x|+3的解析式可化为:
f(x)=
|
易知,当x≥0时,f(x)=(x-1)2+1≥1恒成立,故此时没有零点;当x<0时,令f(x)=0得x=-1或3(舍),故x=-1符合题意;
综上原函数的零点为-1.
(2)当b=-2时,由f(x)<0得,(x-a)|x|<2.
当x=0时,a取任意实数,不等式恒成立;
当0<x≤1时,原式可化为a>x-
| 2 |
| x |
| 2 |
| x |
∴a>gmax(x)=g(1)=-1;
当-1≤x<0时,原式可化为a>x+
| 2 |
| x |
| 2 |
| x |
| 2 |
| x2 |
| 2 |
| 2 |
故函数g(x)在[-1,0)上递减,所以此时a>g(x)max=g(-1)=-3.
综上,当a>-1时对任意x∈[-1,1],f(x)<0恒成立.
点评:本题重点考查了不等式恒成立问题的解法,主要是分离参数,然后转化为求函数的最值问题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知椭圆
+
=1(a>b>0),F为左焦点,A为左顶点,B为上顶点,C为下顶点,且
•
=0,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| CF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=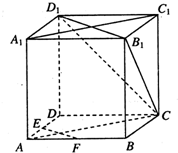 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.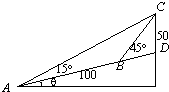 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).