题目内容
已知正三棱锥P-ABC的每个侧面是顶角为30°,腰长为4的三角形,E,F分别是PB,PC上的点,则△AEF的周长的最小值为 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:根据侧面展开图求解得出,再利用直角三角形求解.
解答:
解:∵正三棱锥P-ABC的每个侧面是顶角为30°,腰长为4的三角形,
∴侧面展开为下图

连接AA得:RT△中,长度为4
,
∴△AEF的周长的最小值为4
,
故答案为:4
,
∴侧面展开为下图

连接AA得:RT△中,长度为4
| 2 |
∴△AEF的周长的最小值为4
| 2 |
故答案为:4
| 2 |
点评:本题考查了空间几何体中的最小距离问题,属于中档题.

练习册系列答案
相关题目
已知A为圆A:(x-1)2+y2=25的圆心,平面上点P满足PA=
,那么点P与圆A的位置关系是( )
| 3 |
| A、点P在圆A上 |
| B、点P在圆A内 |
| C、点P在圆A外 |
| D、无法确定 |
已知变量x,y满足约束条件
,则z=3x-y的最大值为( )
|
| A、11 | B、7 | C、3 | D、-5 |
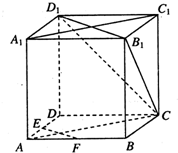 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.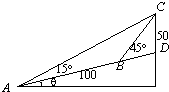 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).