��Ŀ����
��Բx2+
=1��������������˵�ֱ�ΪA��B��ֱ��l�����㣨0��1������Բ������C��D��
��1����l��x�ᡢy��ֱ�������E��F��
=
����ֱ��l�ķ��̣�
��2����ֱ��AD��CB��б�ʷֱ�Ϊk1k2����k1��k2=2��1����k��ֵ��
��3����������C��x1��y1����D��x2��y2�����ֱ��C��D��б��Ϊ-
��-
����ֱ��l1��l2����l1��l2�Ľ���ΪM�����MCD�������Сֵ��
| y2 |
| 4 |
��1����l��x�ᡢy��ֱ�������E��F��
| CE |
| FD |
��2����ֱ��AD��CB��б�ʷֱ�Ϊk1k2����k1��k2=2��1����k��ֵ��
��3����������C��x1��y1����D��x2��y2�����ֱ��C��D��б��Ϊ-
| 4x1 |
| y1 |
| 4x2 |
| y2 |
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������1����C��x1��y1����D��x2��y2����ֱ�ߴ�����Բ���̵ã�4+k2��x2+2kx-3=0�������б�ʽ����ϵ���Ĺ�ϵ���Ƶ�������ֱ��l�ķ���Ϊ2x-y+1=0��2x+y-1=0��
��2��������֪y12=4��1-x12����y22=4��1-x22�����ɴ��Ƴ�3x1x2+5��x1+x2��+3=0������3k2-10k+3=0���ɴ˿��Ƶ���k��ֵ��
��3�����M�Ĺ켣���̣����ͼ�Σ��ɵá�MCD�������Сֵ��
��2��������֪y12=4��1-x12����y22=4��1-x22�����ɴ��Ƴ�3x1x2+5��x1+x2��+3=0������3k2-10k+3=0���ɴ˿��Ƶ���k��ֵ��
��3�����M�Ĺ켣���̣����ͼ�Σ��ɵá�MCD�������Сֵ��
���
�⣺��1����C��x1��y1����D��x2��y2����ֱ��l��y=kx+1
������Բ���̵ã�4+k2��x2+2kx-3=0��
��=4k2+12��4+k2��=16k2+48��
x1+x2=-
��x1x2=-
����֪E��-
��0����F��0��1����
��
=
�����ԣ�-
-x1��-y1��=��x2��y2-1����
����-
-x1=x2����x1+x2=-
����-
=-
�����k=��2���������⣬
���ԣ�����ֱ��l�ķ���Ϊ2x-y+1=0��2x+y-1=0��
��2��k1=
��k2=
��k1��k2=2��1��
����
=2��
ƽ�������x12+
=1������y12=4��1-x12����ͬ��y22=4��1-x22����������ʽ��
�����
=4����3x1x2+5��x1+x2��+3=0��
����3k2-10k+3=0�����k=3��k=
��
��Ϊ
=2��x1��x2�ʣ�-1��1��������y1��y2��ţ�����ȥk=
��
����k=3��
��3����C��x1��y1����D��x2��y2�����ֱ��C��D��б��Ϊ-
��-
����ֱ��l1��l2������Ϊ4x1x+y1y-4=0��4x2x+y2y-4=0����M�Ĺ켣����Ϊy=4��
��y=1�ɵ�x=��
����CD��x��ʱ����MCD�������СֵΪ
��
��3=
��
������Բ���̵ã�4+k2��x2+2kx-3=0��
��=4k2+12��4+k2��=16k2+48��
x1+x2=-
| 2k |
| 4+k2 |
| 3 |
| 4+k2 |
����֪E��-
| 1 |
| k |
��
| CE |
| FD |
| 1 |
| k |
����-
| 1 |
| k |
| 1 |
| k |
����-
| 2k |
| 4+k2 |
| 1 |
| k |
���ԣ�����ֱ��l�ķ���Ϊ2x-y+1=0��2x+y-1=0��
��2��k1=
| y2 |
| x2+1 |
| y1 |
| x1-1 |
����
| y2(x1-1) |
| y1(x2+1) |
ƽ�������x12+
| y12 |
| 4 |
�����
| (1-x2)(1-x1) |
| (1+x1)(1+x2) |
����3k2-10k+3=0�����k=3��k=
| 1 |
| 3 |
��Ϊ
| y2(x1-1) |
| y1(x2+1) |
| 1 |
| 3 |
����k=3��
��3����C��x1��y1����D��x2��y2�����ֱ��C��D��б��Ϊ-
| 4x1 |
| y1 |
| 4x2 |
| y2 |
��y=1�ɵ�x=��
| ||
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
���������⿼��Բ���ߵ��ۺ����ã�������߿������Ҫ����֮һ������ʱҪע�����������������ע����۽��ⷽ����

��ϰ��ϵ�д�
�����Ŀ
��֪ȫ��U={0��1��2��3��4}��M={0��1��2}��N={2��3}����∁UM����N=��������
| A��{2} |
| B��{2��3��4} |
| C��{3} |
| D��{0��1��2��3��4} |
��֪��������{an}����log3an+1=log3an+1��n��N*������a1=1��������{log3an}��ǰn����ǣ�������
A��
| ||
| B��n-1 | ||
C��
| ||
| D��n |
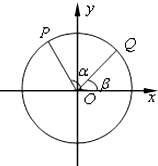 ��ͼ����OxΪʼ�����Ǧ���£�0���£������У������ǵ��ձ߷ֱ��뵥λԲ�ཻ�ڵ�P��Q����֪��P������Ϊ
��ͼ����OxΪʼ�����Ǧ���£�0���£������У������ǵ��ձ߷ֱ��뵥λԲ�ཻ�ڵ�P��Q����֪��P������Ϊ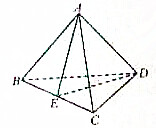 �������ⳤ��Ϊ2��������ABCD�У�E��BC���е㣬д������������ƽ��AED��ֱ���棬��˵�����ɣ�
�������ⳤ��Ϊ2��������ABCD�У�E��BC���е㣬д������������ƽ��AED��ֱ���棬��˵�����ɣ�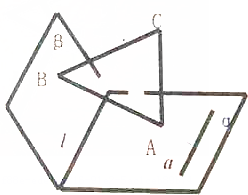 ��ͼ����֪���ɦ�=l��CA�ͦ��ڵ�A��CB�ͦ��ڵ�B��a?����a��AB����֤��a��l��
��ͼ����֪���ɦ�=l��CA�ͦ��ڵ�A��CB�ͦ��ڵ�B��a?����a��AB����֤��a��l��