题目内容
已知函数f(x)=sin2x+2cos2x-1.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)已知△ABC三边a,b,c所对的角分别是A,B,C,若f(
)=
,b=
,且△ABC的面积为1,求a的值.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)已知△ABC三边a,b,c所对的角分别是A,B,C,若f(
| A |
| 2 |
| 2 |
| 2 |
考点:余弦定理,三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:解三角形
分析:(Ⅰ)f(x)解析式利用二倍角的余弦函数公式,以及两角和与差的正弦函数公式化为一个角的正弦函数,利用周期公式求出函数f(x)的最小正周期,根据正弦函数的单调性求出f(x)的单调递增区间即可;
(Ⅱ)由第一问确定出的解析式,根据f(
)=
,求出A的度数,利用三角形面积公式列出关系式,把sinA,b,已知面积代入求出c的值,利用余弦定理求出a的值即可.
(Ⅱ)由第一问确定出的解析式,根据f(
| A |
| 2 |
| 2 |
解答:
解:(Ⅰ)f(x)=sin2x+cos2x=
sin(2x+
),
∵ω=2,∴T=π,
令-
+2kπ≤2x+
≤
+2kπ,k∈Z,解得:-
+kπ≤x≤
+kπ,k∈Z,
则函数f(x)的最小正周期为π,单调递增区间为[-
+kπ,
+kπ],k∈Z;
(Ⅱ)由(Ⅰ)得:f(
)=
sin(A+
)=
,
∴A+
=
,即A=
,
∵S△ABC=
bcsinA=
×
×c×
=1,
∴c=2,
由余弦定理得:a2=b2+c2-2bccosA=2+4-4=2,
解得:a=
.
| 2 |
| π |
| 4 |
∵ω=2,∴T=π,
令-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
则函数f(x)的最小正周期为π,单调递增区间为[-
| 3π |
| 8 |
| π |
| 8 |
(Ⅱ)由(Ⅰ)得:f(
| A |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∴A+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴c=2,
由余弦定理得:a2=b2+c2-2bccosA=2+4-4=2,
解得:a=
| 2 |
点评:此题考查了余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
已知点A(-1,2),B(2,-2),C(0,3),若点M(a,b)(a≠0)是线段AB上一点,则直线CM的斜率的取值范围是( )
A、(-∞,-
| ||
| B、[1,+∞] | ||
C、(-∞,-
| ||
D、[-
|
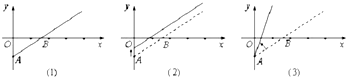 如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法:
如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法: