题目内容
 一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )
一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )A、4π+
| ||||
B、4π+
| ||||
C、2π+
| ||||
D、2π+
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:通过三视图判断几何体的形状,利用三视图的数据求出几何体的表面积即可.
解答:
解:设圆柱底面圆的半径为R,由俯视图,
该圆的内接正三角形的边长为
,由正弦定理得
=2R⇒R=1,
故该几何体的表面积是
圆柱的表面积与三棱锥的侧面积的和减去三棱锥的底面积.
圆柱的表面积是2πR2+2πR•1=4π,
三棱锥的侧面三角形的高为:
=
,
故侧面积为3×
×
×
=
三角形的底面积为
×
×
×
=
.
故选:A.
该圆的内接正三角形的边长为
| 3 |
| ||
| sin60° |
故该几何体的表面积是
圆柱的表面积与三棱锥的侧面积的和减去三棱锥的底面积.
圆柱的表面积是2πR2+2πR•1=4π,
三棱锥的侧面三角形的高为:
(
|
| 3 |
| 2 |
故侧面积为3×
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
9
| ||
| 4 |
三角形的底面积为
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
故选:A.
点评:本题考查组合体的三视图的表面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知双曲线的渐近线方程为x±2y=0,则该双曲线的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
复数z=
(i为虚数单位)的虚部是( )
| 2+i |
| 1-2i |
| A、i | B、1 | C、-1 | D、-i |
设i是虚数单位,复数z1=2-i,z2=1+3i,则z1•z2=( )
| A、-1-5i | B、-1+5i |
| C、5-5i | D、5+5i |
数列{an}中,an+1=
,已知该数列既是等差数列又是等比数列,则该数列的前20项的和等于( )
| an2 |
| 2an-5 |
| A、100 |
| B、0或100 |
| C、100或-100 |
| D、0或-100 |
若复数z满足:(3-i)z=3+i(i为虚数单位),则复数z在复平面内对应的点所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
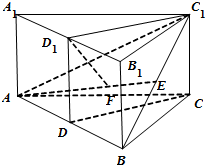 如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.