题目内容
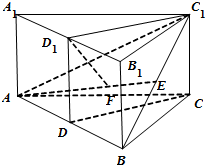 如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.(1)求证:平面ABC1⊥平面DCC1D1;
(2)若D1在平面ABC1的射影F在边AE上,且
| AA 1 |
| AB |
| 1 |
| 2 |
考点:直线与平面所成的角,平面与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用线面垂直的判定定理和性质定理,以及面面垂直的判定定理即可证得;
(2)由(1)的结论和D1在平面ABC1的射影F在边AE上,得到F为△ABC1的重心,运用射影定理知,D1C1=
DD1
设DD1=a,求出D1F、AD1的长,由直线与平面所成的角的定义得到∠D1AF是所成的角,求出正弦值即可.
(2)由(1)的结论和D1在平面ABC1的射影F在边AE上,得到F为△ABC1的重心,运用射影定理知,D1C1=
| 2 |
设DD1=a,求出D1F、AD1的长,由直线与平面所成的角的定义得到∠D1AF是所成的角,求出正弦值即可.
解答:
(1)证明:∵ CA=CB,D为AB的中点,∴CD⊥AB,
CA=CB,D为AB的中点,∴CD⊥AB,
∵CC1⊥平面ABC,∴CC1⊥AB,∴AB⊥平面DCC1D1,
∵AB?平面ABC1,∴平面ABC1⊥平面DCC1D1;
(2)解:由(1)平面ABC1⊥平面DCC1D1,
∴D1在平面ABC1上的射影F在交线C1D上,
已知F也在AE上,且C1D,AE为△ABC1的中线,
∴F为△ABC1的重心,且
=2
,
∵在△DD1C1中,∠DD1C1为直角,D1F⊥DC1,
利用射影定理知,D1C1=
DD1,设DD1=a,则D1C1=
a,D1F=
a,AD=a,AD1=
a,
∴sin∠D1AF=
=
,即直线AD1与平面ABC1所成的角的正弦值为
.
 CA=CB,D为AB的中点,∴CD⊥AB,
CA=CB,D为AB的中点,∴CD⊥AB,∵CC1⊥平面ABC,∴CC1⊥AB,∴AB⊥平面DCC1D1,
∵AB?平面ABC1,∴平面ABC1⊥平面DCC1D1;
(2)解:由(1)平面ABC1⊥平面DCC1D1,
∴D1在平面ABC1上的射影F在交线C1D上,
已知F也在AE上,且C1D,AE为△ABC1的中线,
∴F为△ABC1的重心,且
| C1F |
| FD |
∵在△DD1C1中,∠DD1C1为直角,D1F⊥DC1,
利用射影定理知,D1C1=
| 2 |
| 2 |
| ||
| 3 |
| 2 |
∴sin∠D1AF=
| ||||
|
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查空间直线与平面的位置关系,考查直线与平面垂直的判定和性质,以及面面垂直的判定,同时考查空间的角:直线与平面所成的角,考查基本的运算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )
一个几何体是由圆柱和正三棱锥组合而成,其正视图和俯视图如图所示,则该几何体的表面积是( )A、4π+
| ||||
B、4π+
| ||||
C、2π+
| ||||
D、2π+
|
 如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=
如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=